Tag Archives: TensorFlow

The Power of Open Source


At the day 1 keynote of Open Source Summit North America, Timothy Jordan, Director of Developer Relations and Open Source at Google, will talk about the landscape of open source and AI, the importance of a responsible approach, and the transformative impact of community collaboration. In anticipation of this talk, let’s break down the AI open source ecosystem, and how Google approaches it.

Google believes in the power of open technology to drive innovation and benefit everyone. It fosters creativity and collaboration, while ensuring technology access for developers and allowing customization to fit unique use cases. Open source licenses give developers full creative autonomy without restriction. It is this ecosystem of open source and open technology, shaped by ML frameworks like TensorFlow, Keras, and JAX, that has enabled so many incredible advances in AI in recent years.

The open source community has been in discussion on how to apply the Open Source Definition to carry forward the open principles of the OSD while addressing concepts like derived work and author attribution in AI. During Timothy’s keynote, he’ll speak to his own philosophy on Open Source and AI, and share how his assumptions about how we apply open source to AI have evolved. The immediate availability of AI models, powered by the open source ecosystem of ML frameworks, means it’s more important than ever that we establish a shared definition for open source and AI.

While that definition is in development, at Google we’re using precise language to describe our openly available models like Gemma. The definition and license is only one part of this open ML/AI future; advancements in safety tooling, policies, and developer knowledge are all part of creating a responsible and open future for AI. Those advancements are all fueled by a dedication to collaboration. Whether sharing innovations and improvements with the community, or having conversations with policymakers and open source leaders, collaboration is key to a responsible approach to AI in the open ecosystem. AI can only be safe and responsible if everyone’s experiences and perspectives are brought to the forefront as it’s built.

To demonstrate how open source has made AI readily available, Timothy will also take the audience through a “low code” demo of how to run large language models in-browser for web applications. Using MediaPipe, the LLM Inference API, and Gemma, users can quickly add genAI capabilities like document summarization and text generation.

Join us at Open Source Summit North America for this keynote, and visit opensource.google to learn more.

By the Google Open Source team

Graph neural networks in TensorFlow

Posted by Dustin Zelle, Software Engineer, Google Research, and Arno Eigenwillig, Software Engineer, CoreML

Objects and their relationships are ubiquitous in the world around us, and relationships can be as important to understanding an object as its own attributes viewed in isolation — take for example transportation networks, production networks, knowledge graphs, or social networks. Discrete mathematics and computer science have a long history of formalizing such networks as graphs, consisting of nodes connected by edges in various irregular ways. Yet most machine learning (ML) algorithms allow only for regular and uniform relations between input objects, such as a grid of pixels, a sequence of words, or no relation at all.

Graph neural networks, or GNNs for short, have emerged as a powerful technique to leverage both the graph’s connectivity (as in the older algorithms DeepWalk and Node2Vec) and the input features on the various nodes and edges. GNNs can make predictions for graphs as a whole (Does this molecule react in a certain way?), for individual nodes (What’s the topic of this document, given its citations?) or for potential edges (Is this product likely to be purchased together with that product?). Apart from making predictions about graphs, GNNs are a powerful tool used to bridge the chasm to more typical neural network use cases. They encode a graph's discrete, relational information in a continuous way so that it can be included naturally in another deep learning system.

We are excited to announce the release of TensorFlow GNN 1.0 (TF-GNN), a production-tested library for building GNNs at large scales. It supports both modeling and training in TensorFlow as well as the extraction of input graphs from huge data stores. TF-GNN is built from the ground up for heterogeneous graphs, where types of objects and relations are represented by distinct sets of nodes and edges. Real-world objects and their relations occur in distinct types, and TF-GNN's heterogeneous focus makes it natural to represent them.

Inside TensorFlow, such graphs are represented by objects of type tfgnn.GraphTensor. This is a composite tensor type (a collection of tensors in one Python class) accepted as a first-class citizen in tf.data.Dataset, tf.function, etc. It stores both the graph structure and its features attached to nodes, edges and the graph as a whole. Trainable transformations of GraphTensors can be defined as Layers objects in the high-level Keras API, or directly using the tfgnn.GraphTensor primitive.


GNNs: Making predictions for an object in context

For illustration, let’s look at one typical application of TF-GNN: predicting a property of a certain type of node in a graph defined by cross-referencing tables of a huge database. For example, a citation database of Computer Science (CS) arXiv papers with one-to-many cites and many-to-one cited relationships where we would like to predict the subject area of each paper.

Like most neural networks, a GNN is trained on a dataset of many labeled examples (~millions), but each training step consists only of a much smaller batch of training examples (say, hundreds). To scale to millions, the GNN gets trained on a stream of reasonably small subgraphs from the underlying graph. Each subgraph contains enough of the original data to compute the GNN result for the labeled node at its center and train the model. This process — typically referred to as subgraph sampling — is extremely consequential for GNN training. Most existing tooling accomplishes sampling in a batch way, producing static subgraphs for training. TF-GNN provides tooling to improve on this by sampling dynamically and interactively.

Pictured, the process of subgraph sampling where small, tractable subgraphs are sampled from a larger graph to create input examples for GNN training.

TF-GNN 1.0 debuts a flexible Python API to configure dynamic or batch subgraph sampling at all relevant scales: interactively in a Colab notebook (like this one), for efficient sampling of a small dataset stored in the main memory of a single training host, or distributed by Apache Beam for huge datasets stored on a network filesystem (up to hundreds of millions of nodes and billions of edges). For details, please refer to our user guides for in-memory and beam-based sampling, respectively.

On those same sampled subgraphs, the GNN’s task is to compute a hidden (or latent) state at the root node; the hidden state aggregates and encodes the relevant information of the root node's neighborhood. One classical approach is message-passing neural networks. In each round of message passing, nodes receive messages from their neighbors along incoming edges and update their own hidden state from them. After n rounds, the hidden state of the root node reflects the aggregate information from all nodes within n edges (pictured below for n = 2). The messages and the new hidden states are computed by hidden layers of the neural network. In a heterogeneous graph, it often makes sense to use separately trained hidden layers for the different types of nodes and edges

Pictured, a simple message-passing neural network where, at each step, the node state is propagated from outer to inner nodes where it is pooled to compute new node states. Once the root node is reached, a final prediction can be made.

The training setup is completed by placing an output layer on top of the GNN’s hidden state for the labeled nodes, computing the loss (to measure the prediction error), and updating model weights by backpropagation, as usual in any neural network training.

Beyond supervised training (i.e., minimizing a loss defined by labels), GNNs can also be trained in an unsupervised way (i.e., without labels). This lets us compute a continuous representation (or embedding) of the discrete graph structure of nodes and their features. These representations are then typically utilized in other ML systems. In this way, the discrete, relational information encoded by a graph can be included in more typical neural network use cases. TF-GNN supports a fine-grained specification of unsupervised objectives for heterogeneous graphs.


Building GNN architectures

The TF-GNN library supports building and training GNNs at various levels of abstraction.

At the highest level, users can take any of the predefined models bundled with the library that are expressed in Keras layers. Besides a small collection of models from the research literature, TF-GNN comes with a highly configurable model template that provides a curated selection of modeling choices that we have found to provide strong baselines on many of our in-house problems. The templates implement GNN layers; users need only to initialize the Keras layers.

At the lowest level, users can write a GNN model from scratch in terms of primitives for passing data around the graph, such as broadcasting data from a node to all its outgoing edges or pooling data into a node from all its incoming edges (e.g., computing the sum of incoming messages). TF-GNN’s graph data model treats nodes, edges and whole input graphs equally when it comes to features or hidden states, making it straightforward to express not only node-centric models like the MPNN discussed above but also more general forms of GraphNets. This can, but need not, be done with Keras as a modeling framework on the top of core TensorFlow. For more details, and intermediate levels of modeling, see the TF-GNN user guide and model collection.


Training orchestration

While advanced users are free to do custom model training, the TF-GNN Runner also provides a succinct way to orchestrate the training of Keras models in the common cases. A simple invocation may look like this:

The Runner provides ready-to-use solutions for ML pains like distributed training and tfgnn.GraphTensor padding for fixed shapes on Cloud TPUs. Beyond training on a single task (as shown above), it supports joint training on multiple (two or more) tasks in concert. For example, unsupervised tasks can be mixed with supervised ones to inform a final continuous representation (or embedding) with application specific inductive biases. Callers only need substitute the task argument with a mapping of tasks:

Additionally, the TF-GNN Runner also includes an implementation of integrated gradients for use in model attribution. Integrated gradients output is a GraphTensor with the same connectivity as the observed GraphTensor but its features replaced with gradient values where larger values contribute more than smaller values in the GNN prediction. Users can inspect gradient values to see which features their GNN uses the most.


Conclusion

In short, we hope TF-GNN will be useful to advance the application of GNNs in TensorFlow at scale and fuel further innovation in the field. If you’re curious to find out more, please try our Colab demo with the popular OGBN-MAG benchmark (in your browser, no installation required), browse the rest of our user guides and Colabs, or take a look at our paper.


Acknowledgements

The TF-GNN release 1.0 was developed by a collaboration between Google Research: Sami Abu-El-Haija, Neslihan Bulut, Bahar Fatemi, Johannes Gasteiger, Pedro Gonnet, Jonathan Halcrow, Liangze Jiang, Silvio Lattanzi, Brandon Mayer, Vahab Mirrokni, Bryan Perozzi, Anton Tsitsulin, Dustin Zelle, Google Core ML: Arno Eigenwillig, Oleksandr Ferludin, Parth Kothari, Mihir Paradkar, Jan Pfeifer, Rachael Tamakloe, and Google DeepMind: Alvaro Sanchez-Gonzalez and Lisa Wang.

Source: Google AI Blog


Global developers use Google tools to build solutions in recruiting, mentorship and more

Posted by Lyanne Alfaro, DevRel Program Manager, Google Developer Studio

Developer Journey is a monthly series highlighting diverse and global developers sharing relatable challenges, opportunities, and wins in their journey. Every month, we will spotlight developers around the world, the Google tools they leverage, and the kinds of products they are building.

This month we speak with global developers across Google Developer Experts, and Women Techmakers, to learn more about their favorite Google tools, the applications they’ve built to serve diverse communities and the role of inclusive design in their process.

Miguel Ángel Durán Garcí

Headshot of Miguel Ángel Durán Garcí, smiling
Barcelona, Spain
Google Developer Expert, Web Technologies
Content Creator & Software Engineer

What Google tools have you used to build?

I've been using Firebase, Google Cloud Platform, CrUX Dashboard, and Chrome DevTools for years. As a web developer, I'm always excited about the new features that DevTools brings to us to improve our productivity and the performance of our applications.


Which tool has been your favorite to use? Why?

Lately, I've been trying Project IDX, an entirely web-based workspace for full-stack application development, and I'm really excited about the future of this project. I love the idea of being able to develop and deploy applications from the browser, without having to install anything on my computer.


Please share with us about something you’ve built in the past using Google tools.

Most recently, I've deployed AdventJS, a holiday calendar for developers. For optimizing the images, I've used Squoosh from the GoogleChromeLabs team. To ensure the website was accessible and to tweak performance, I've used Lighthouse from Chrome DevTools. Also, I used Google Bard to translate the content of the website into English and Portuguese.


What will you create with Google Bard?

I'm planning to expand a website I've created for the Spanish-speaking community to teach JavaScript from scratch. With Google Bard, I can check the content, create some code, and make it help me create challenges for the students.


What advice would you give someone starting in their developer journey?

I would tell them to be patient and to enjoy the process. It's a long journey, but it's worth it. Also, I would tell them to be curious and avoid sticking to only a few technologies. And finally, I would tell them to share their knowledge with the community, because it's the best way to learn and meet new people. You don't need to be an expert to share your knowledge; you just need to be one step ahead of the people you're teaching.

Marian Villa

Headshot of Marian Villa, smiling
Medellín, Colombia
Google Developer Expert, Web Technologies
Co-founder / Director Pionerasdev

What Google tools have you used to build?

Development and Creativity:

  • Google Chrome DevTools
  • Bard
  • TensorflowJS

Productivity and Communication:

  • Gmail
  • Google Calendar
  • Google Drive
  • Google Docs
  • Google Sheets
  • Google Slides
  • Google Meet

Marketing and Business:

  • Google Ads
  • Google Analytics
  • Google My Business
  • Google Workspace
  • Google Cloud Platform
  • Google Marketing Platform

Education and Learning:

  • Google Classroom
  • Google Forms
  • Google Sites
  • YouTube

Which tool has been your favorite to use? Why?

Choosing a favorite tool is quite a task given the unique strengths of Bard, TensorflowJS and Google Chrome DevTools, but I'd have to say that Google Chrome DevTools stands out for me. Its versatility in inspecting and debugging web pages, testing code variations, and providing insights into JavaScript behavior has been crucial in my web development endeavors. That being said, both Bard and TensorFlow.js have incredible capabilities. Bard plays a vital role in generating creative content, answering queries, and even composing code. TensorFlow.js, on the other hand, is a game-changer, enabling machine learning in JavaScript, and making it accessible for a wide range of applications. Each tool has its unique appeal, and the choice will depend on the context and specific requirements of the task at hand.


Please share with us about something you’ve built in the past using Google tools.

On our latest website, we use all the Google technologies at hand to enhance our image as an NGO. Find it here.


What will you create with Google Bard?

We are once again resuming a winning mentorship project to advance our career as developers, so Bard and Duet AI are great allies to inspect our code and once again create an MVP of this product for our community.


What advice would you give someone starting in their developer journey?

First, think about the problem you want to solve, or what you want to contribute to the world, then create and make it come true. This is easier if you rely on communities, and people who help you as mentors, sponsors and guides.

Rubens de Almeida Zimbres

Headshot of Rubens Zimbres, smiling
São Paulo - Brazil
Google Developer Expert, Machine Learning and Google Cloud
ML Engineer

What Google tools have you used to build?

I’ve been using the full stack of Google Products. I use Google Workspace daily in my life, my personal website is made on Google Sites, and Google Cloud; I started with Compute Engine and Jupyter Notebooks, customized to my needs.

As I acquired more knowledge through practical experience, Coursera and Google Cloud Skills Boost, I started building end to-end solutions using BigQuery, SQL, lots of Vertex AI (Generative AI Studio, Matching Engine, Speech-to-text, Pipelines, AutoML, Model Fine-Tuning), Cloud Run (and a little GKE - Kubernetes), Cloud Functions, Dialogflow and Document AI.

As the requirements of clients change according to the industry, like recruiting (Virtual Career Center) and contact center (Contact Center AI), I was able to test and deploy in production different Google products to solve the clients’ needs.


Which tool has been your favorite to use? Why?

Vertex AI is my favorite, as it is pure ML and Deep Learning optimized. Using AutoML with NAS (Neural Architecture Search) was a very interesting experience with awesome results. Developing Machine Learning pipelines with Kubeflow is a special pleasure, as this is going into production and the whole MLOps is involved.


Please share with us about something you’ve built in the past using Google tools.

I’ve built a recruiting solution that was implemented in six countries of Latin America, benefiting more than 365,000 people. This solution automatically analyzes resumes using OCR via Document AI.

I delivered a revenue prediction for a hotel chain using Tensorflow, where we increased the accuracy of the client’s model by 0.95%. I also built a Contact Center solution which uses Google Speech-to-Text and analytics to make management easier and also to generate strategic insights.

Lately, I was part of the team that delivered an end-to-end Virtual Career Center solution that matches job candidates to job vacancies using Vertex AI Matching Engine via text embeddings and SCANN. Both the recruiting solution and the contact center solution generated patents in Brazil, in the field of NLP (Natural Language Processing).


What will you create with Google Bard?

Google Bard is part of my daily routine. It helps me while coding, it helps me to plan trips, get to the right public transportation, visit interesting places around the world and it also helps by retrieving the Google search in an organized way, with updated content. My idea is to use Bard along with LangChain to perform optimizations in the finance industry.


What advice would you give someone starting in their developer journey?

Learn the basics first.

The temptation of learning this magnificent field as Machine Learning is gigantic, but coding is a great part of the solution. Learn to code properly, in whatever language you want. This brings efficiency and security if your solution needs to scale, decreasing infrastructure costs and improving user experience.

The same applies to Machine Learning: learn basic disciplines such as Calculus, Computer Science fundamentals and you will understand most of the content is shared today online. Only after learning ML you should dive into Deep Learning and the disciplines associated. Don’t fake it. Make it.

Global Google Developer Experts Share Their Favorite Tools and Advice for New Developers

Posted by Lyanne Alfaro, DevRel Program Manager, Google Developer Studio

Developer Journey is a monthly series highlighting diverse and global developers sharing relatable challenges, opportunities, and wins in their journey. Every month, we will spotlight developers around the world, the Google tools they leverage, and the kinds of products they are building.

This month we speak with global Google Developer Experts in Firebase, Women Techmakers, and beyond, to learn more about their favorite Google tools, the applications they’ve built to serve diverse communities, and their best advice for anyone just getting started as a developer.

Juan Lombana

Headshot of Juan Lombana, smiling
Mexico City, Mexico
Founder, Mercatitlán

What Google tools have you used to build?

Google Analytics and Firebase's A/B testing features have been pivotal in our data-driven approach, enabling continuous improvement in our conversion strategies. More recently, Bard has become a significant asset in developing new products and in our educational endeavors, especially with the introduction of our AI course. Its utility in both product development and educational settings is profound.


Which tool has been your favorite to use? Why?

If I had to choose, it would be Google Ads. Its ability to consistently drive new customers and provide unparalleled visibility to quality products is unmatched. While it may not traditionally be considered a 'tool' in the strictest sense, its impact on business growth and visibility is indisputable.


Please share with us about something you’ve built in the past using Google tools.

My entire business, Mercatitlán, has been built and scaled using Google Tools. We have cultivated a community of over 40,000 paid students, educating them on effective use of Google Ads, leveraging Bard for enhanced website content, and employing Google Analytics for strategic A/B testing to boost sales. The transformational impact of these tools on both my business and my students' ventures is a testament to their potential.


What will you create with Google Bard?

The integration of Bard AI into our daily operations is revolutionizing the way we approach digital marketing. Beyond its current uses in social media content creation, ad ideas generation, email composition, and customer support enhancement, we're exploring several innovative applications:

  • Personalized Marketing Campaigns: Using Bard AI, we can analyze customer data and preferences to create highly personalized marketing campaigns. This helps in delivering more relevant content to our audience, thereby increasing engagement and conversion rates. 
  • Competitive Analysis: By analyzing competitor data, Bard AI can help us understand their strategies, strengths, and weaknesses. This intelligence is crucial for refining our marketing approach and differentiating our brand in the marketplace.
  • Content Optimization for SEO: Bard can assist in optimizing website and blog content for search engines. By understanding and integrating key SEO principles, it can help us rank higher in search results, thus improving our online visibility. 
  • Automated Reporting and Insights: Automating the generation of marketing reports and insights with Bard saves time and resources, allowing our team to focus on strategy and creativity rather than manual data analysis.

What advice would you give someone starting in their developer journey?

The key is to start with action rather than waiting for perfection. Adopt a mindset focused on experimentation and analytics. This approach allows you to follow data-driven insights rather than solely relying on innovation, leading to significant societal impact through technology.

Jirawat Karanwittayakarn

Headshot of Jirawat Karanwittayakarn, smiling
Bangkok, Thailand
Tech Evangelist, LINE Thailand

What Google tools have you used to build?

I have used a variety of Firebase services to build LINE chatbots for a number of years. These services have included Cloud Functions, Cloud Firestore, Cloud Storage, Firebase Hosting, and etc. Recently I have also used the PaLM API, a very powerful tool that allows me to build Generative AI chatbots.


Which tool has been your favorite to use? Why?

Firebase is my favorite tool because it is a platform that provides a complete set of tools for building and managing mobile, web, and chatbots. It is very easy to use and has a wide range of features that make it a great choice for developers of all levels. Furthermore, Firebase services have allowed me to scale my chatbots and make them more reliable.


Please share with us about something you’ve built in the past using Google tools.

  • LINE Developers TH is a chatbot that allows Thai developers to learn about LINE APIs and get started with building services. It also provides users with the ability to try out demos of LINE APIs.
  • TrueMoney is a wallet app that I have built in the past using Firebase. The app allows users to store money, send money, and pay bills. It is a very popular app in Thailand, with over 10 million users.
  • Sanook is an app that allows users to access news, articles, and other content from the number one web portal in Thailand on their mobile devices.

What will you create with Google Bard?

I would like to create a use case of building a powerful LINE chatbot using PaLM API and Firebase for developers. I believe this will be a great way to showcase the power of these tools and how they can be used to create innovative solutions.


What advice would you give someone starting in their developer journey?

First and foremost, I would encourage them to be curious and always be willing to learn new things. The world of technology is constantly changing, so it's important to stay up-to-date on the latest trends and technologies. This can be done by reading articles, attending conferences, and taking online courses.

Secondly, I would recommend that they find a mentor or role model who can help guide them on their journey. Having someone who has been through the process can be invaluable in providing support and advice. They can help you identify areas where you need to improve, and provide you with tips and tricks for success.

Finally, I would encourage them to never give up. The road to becoming a developer can be challenging, but it's also incredibly rewarding. If you're passionate about technology, then don't let anything stop you from pursuing your dreams.

Laura Morinigo

Headshot of Lauren Moringo, smiling
London, England
Women Techmakers Ambassador
Principal Engineer and Consultant, Samsung Electronics UK

What Google tools have you used to build?

I have used tools like Google Cloud and Firebase.


Which tool has been your favorite to use? Why?

I would say Firebase! It helped me to build web apps and explore new technologies easily while saving a lot of time and resources. Additionally, a lot of functionalities have been added recently. Over the years, I've witnessed its evolution, with the addition of numerous functionalities that continually enhance its utility and user experience. This constant innovation within Firebase not only simplifies complex tasks but also opens doors to creative possibilities in web app development.


Please share with us about something you’ve built in the past using Google tools.

I've been leading a project in partnership with the United Nations to help share information about its worldwide global goals. We used Firebase hosting and Cloud functions for the first release of the web app and it was a success! It felt very good to help create tools that support a good cause.


What will you create with Google Bard?

I'm experimenting with the current extensions to improve personal productivity. It's very interesting how you can improve the way that you do your daily tasks.


What advice would you give someone starting in their developer journey?

Remember that as a developer you will have the power to create! Use this power to build personal projects and combine it with things that you enjoy. You will start building a portfolio and have fun while learning. Finally, don't hesitate to find a mentor and connect with a community of developers to support and guidance in your journey. You can find a lot of help, improve your networking, and even have friends for life!

Global Developers Share How They Use Inclusive Design

Posted by Lyanne Alfaro, DevRel Program Manager, Google Developer Studio

Developer Journey is a monthly series highlighting diverse and global developers sharing relatable challenges, opportunities, and wins in their journey. Every month, we will spotlight developers around the world, the Google tools they leverage, and the kind of products they are building.

This month we speak with global developers across Google Developer Experts, Google Developer Groups, and beyond to learn more about their favorite Google tools, the applications they’ve built to serve diverse communities and the role of inclusive design in their process.

Lamis Chebbi

Headshot of Lamis Chebbi, smiling
Republic of Tunisia
Senior Software Engineer

What Google tools have you used to build?

I use Lighthouse and Google PageSpeed Insights to audit my application's performance and check my accessibility score. I can learn a lot about my application users and measure their engagement through Google Analytics. I have also used: Angular, Angular Dev tools, Firebase, TensorFlow and some services through Google Cloud Platform.


Which tool has been your favorite to use? Why?

On a daily basis I use Angular to develop my web applications. It helped me develop web applications faster with less code, less debugging time, and high scalability. The Angular CLI automates a lot of tasks, including the upgrade process, which saves a lot of time.


Please share with us about something you’ve built in the past using Google tools.

I have built a lot of web apps and progressive web apps using Angular, Firebase and TensorFlow in various fields from insurance, to banking, retail and education.


What will you create with Google Bard?

I'm planning on creating a blog using Google Bard and to generate content in different languages and enable some search and updates for content.


What role does inclusive design play in your development process?

Accessibility is no longer an option today. It is as important as other development goals and should be automated in the development process using the right tools.


What advice would you give someone starting in their developer journey?

Here’s a few pieces of advice for other professionals:

  • Invest in learning as much as you can and always practice the technologies you learn.
  • Don't forget that practice makes perfect.
  • Join developer communities and get a mentor; you will learn a lot and receive a lot of help.
  • Try to keep up with new technologies and trends that will open new perspectives for you.

You’ll probably make some mistakes. Be willing to accept it and learn from it.

Amani Bisimwa

Headshot of Amani Bisimwa, smiling
Bukavu, Democratic Republic of Congo
Google Developer Groups Uvira Lead
Frontend Developer

What Google tools have you used to build?

I am using Angular and Firebase.


Which tool has been your favorite to use? Why?

Firebase is my favorite. I like how Firebase has simplified things by providing a Backend as Service. You no longer need to manage your own servers, worry about scalability, or other Backend complexities.


Please share with us about something you’ve built in the past using Google tools.

I have built some private ERP apps that help small local traders to manage their business (stock management, finance and hotels).


What will you create with Google Bard?

I always use Bard for guidance to document and test code. I hope to use it for more projects in the future.


What role does inclusive design play in your development process?

The role of a designer in the development process is so important to me. Not only does it allow me to arrange the elements well on the screen, but it also ensures that the application is accessible to users living with disabilities. The designer also knows how to choose colors, contrasts and hierarchy of different elements.


How do you prioritize accessibility alongside other development goals?

Accessibility is a priority for me when creating an app or product. I consider accessibility at every stage of the development process. I use a variety of tools and resources to ensure my apps are accessible to everyone, including people with visual impairments, hearing impairments, motor disabilities and cognitive disabilities.


What advice would you give someone starting in their developer journey?

My advice is: Choose your path and stick to it because there are several distractions from the trends of new technologies on social media especially on Twitter. Don't skip the steps; learn the fundamentals.  It's important because even to improve a prompt with generative AI, you need to have a solid understanding in your field.


Enrique López Mañas

Headshot of Enrique López Mañas, smiling
Munich, Germany
Freelance Software Engineer

What Google tools have you used to build?

Android Studio is my daily tool. I have used other tools or frameworks (like Firebase or TensorFlow) in the past as well. My choice of tool depends on the needs of the project I am currently engaged with.


Which tool has been your favorite to use? Why?

Android Studio is my absolute favorite, which is not a surprise for an Android Developer.


Please share with us about something you’ve built in the past using Google tools.

I have worked in many apps and frameworks in the past. The Deutsche Bahn (German Train) application, a Corona app for the Arab Emirates, the app for Alibaba couriers in Vietnam, and now the Google Maps library for Compose.


What will you create with Google Bard?

Bard and other tools like ChatGPT help me with the development of apps and software in general. I do feel they are not yet ready to significantly impact the development process. They still suffer from many inaccuracies and hallucinations.


How do you prioritize accessibility alongside other development goals?

Much less than I would actually like to. Often companies are on a budget and some important things tend to get deprioritized. As a developer (and consultant) my role is to advise them, and A11y is one of the main topics that tend to be underrated.

For instance, do you know that approximately 20% of the users in Switzerland have some form of disability, and can benefit from apps with accessibility integrated? I was really surprised when I heard this number, and I am fairly confident most people don't know about it. If there were more awareness, apps would benefit more from A11y practices.


What advice would you give someone starting in their developer journey?

For new developers: ask all the questions. Never leave a room with a doubt or a question and without an answer. Even more senior people do not have all the answers all the time, and the only way to know if they do is to ask questions. Do not feel embarrassed by raising your hand in a meeting. Ask all the questions you need. The quality of your life will be determined by the quality of your questions.

Machine Learning Communities: Q2 ‘23 highlights and achievements

Posted by Nari Yoon, Bitnoori Keum, Hee Jung, DevRel Community Manager / Soonson Kwon, DevRel Program Manager

Let’s explore highlights and accomplishments of vast Google Machine Learning communities over the second quarter of 2023. We are enthusiastic and grateful about all the activities by the global network of ML communities. Here are the highlights!

ML Training Campaigns Summary

More than 35 communities around the world have hosted ML Campaigns distributed by the ML Developer Programs team during the first half of the year. Thank you all for your training efforts for the entire ML community!


Community Highlights


Keras

Screengrab of Tensorflow & Deep Learning Malaysia June 2023 Webinar - 'KerasCV for the Young and Restless'

Image Segmentation using Composable Fully-Convolutional Networks by ML GDE Suvaditya Mukherjee (India) is a Kears.io example explaining how to implement a fully-convolutional network with a VGG-16 backend and how to use it for performing image segmentation. His presentation, KerasCV for the Young and Restless (slides | video) at TFUG Malaysia and TFUG Kolkata was an introduction to KerasCV. He discussed how basic computer vision components work, why Keras is an important tool, and how KerasCV builds on top of the established TFX and Keras ecosystem.

[ML Story] My Keras Chronicles by ML GDE Aritra Roy Gosthipaty (India) summarized his story of getting into deep learning with Keras. He included pointers as to how one could get into the open source community. Plus, his Kaggle notebook, [0.11] keras starter: unet + tf data pipeline is a starter guide for Vesuvius Challenge. He and Subvaditya also shared Keras implementation of Temporal Latent Bottleneck Networks, proposed in the paper.

KerasFuse by ML GDE Ayse Ayyuce Demirbas (Portugal) is a Python library that combines the power of TensorFlow and Keras with various computer vision techniques for medical image analysis tasks. It provides a collection of modules and functions to facilitate the development of deep learning models in TensorFlow & Keras for tasks such as image segmentation, classification, and more.

TensorFlow at Google I/O 23: A Preview of the New Features and Tools by TFUG Ibadan explored the preview of the latest features and tools in TensorFlow. They covered a wide range of topics including Dtensor, KerasCV & KerasNLP, TF quantization API, and JAX2TF.

StableDiffusion- Textual Inversion app

StableDiffusion - Textual-Inversion implementation app by ML GDE Dimitre Oliveira (Brazil) is an example of how to implement code from research and fine-tunes it using the Textual Inversion process. It also provides relevant use cases for valuable tools and frameworks such as HuggingFace, Gradio, TensorFlow serving, and KerasCV.

In Understanding Gradient Descent and Building an Image Classifier in TF From Scratch, ML GDE Tanmay Bakshi (Canada) talked about how to develop a solid intuition for the fundamentals backing ML tech, and actually built a real image classification system for dogs and cats, from scratch in TF.Keras.

TensorFlow and Keras Implementation of the CVPR 2023 paper by Usha Rengaraju (India) is a research paper implementation of BiFormer: Vision Transformer with Bi-Level Routing Attention.

Smile Detection with Python, OpenCV, and Deep Learning by Rouizi Yacine is a tutorial explaining how to use deep learning to build a more robust smile detector using TensorFlow, Keras, and OpenCV.


Kaggle

Screengrab of ML Olympiad for Students - TopVistos USA

ML Olympiad for Students by GDSC UNINTER was for students and aspiring ML practitioners who want to improve their ML skills. It consisted of a challenge of predicting US working visa applications. 320+ attendees registered for the opening event, 700+ views on YouTube, 66 teams competed, and the winner got a 71% F1-score.

ICR | EDA & Baseline by ML GDE Ertuğrul Demir (Turkey) is a starter notebook for newcomers interested in the latest featured code competition on Kaggle. It got 200+ Upvotes and 490+ forks.

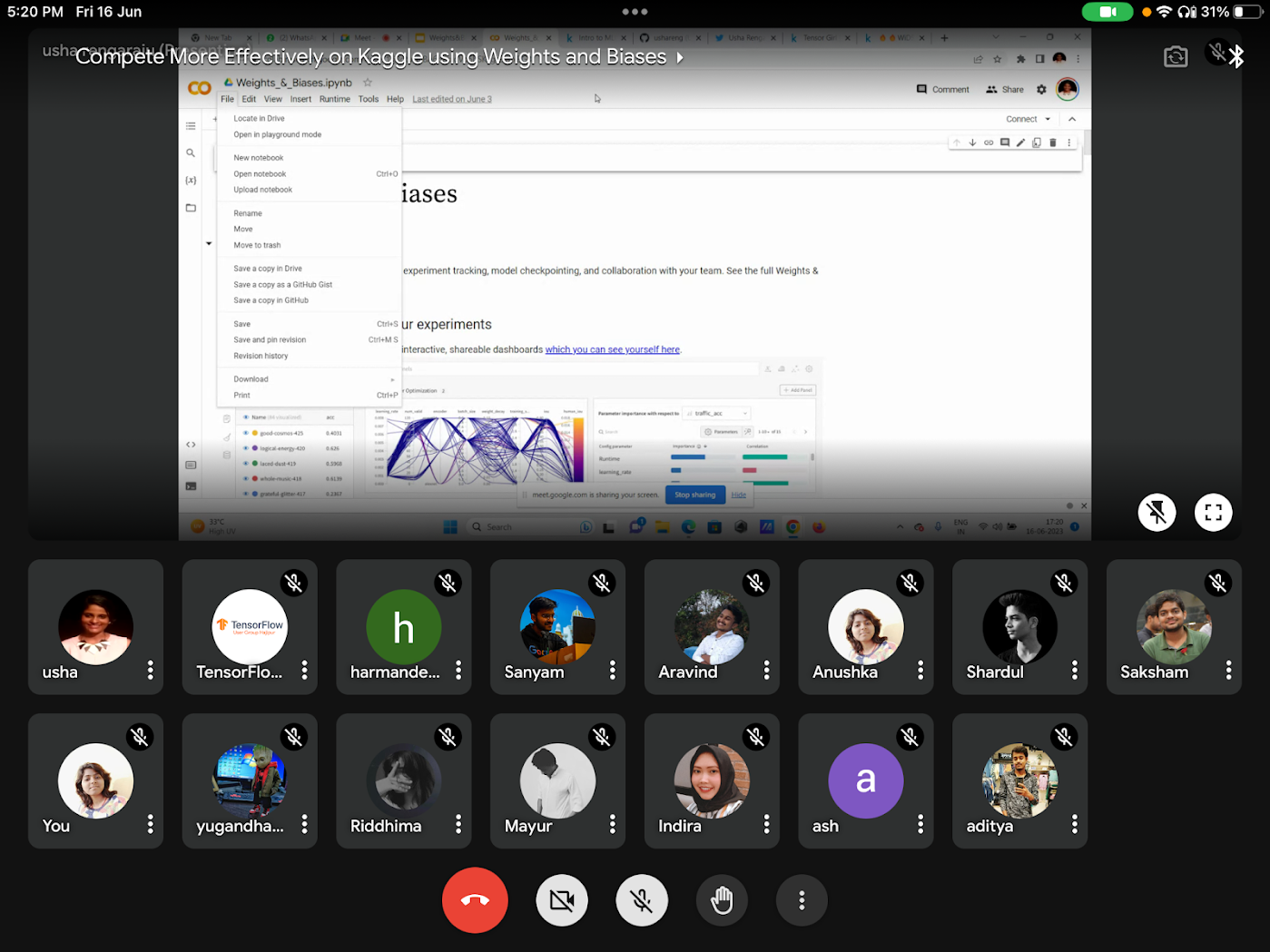
Screengrab of Compete More Effectively on Kaggle using Weights and Biases showing participants in the video call

Compete More Effectively on Kaggle using Weights and Biases by TFUG Hajipur was a meetup to explore techniques using Weights and Biases to improve model performance in Kaggle competitions. Usha Rengaraju (India) joined as a speaker and delivered her insights on Kaggle and strategies to win competitions. She shared tips and tricks and demonstrated how to set up a W&B account and how to integrate with Google Colab and Kaggle.

Skeleton Based Action Recognition: A failed attempt by ML GDE Ayush Thakur (India) is a discussion post about documenting his learnings from competing in the Kaggle competition, Google - Isolated Sign Language Recognition. He shared his repository, training logs, and ideas he approached in the competition. Plus, his article Keras Dense Layer: How to Use It Correctly) explored what the dense layer in Keras is and how it works in practice.


On-device ML

Google for developers Edu Program Tech Talks for Educators Add Machine Learning to your Android App June 22, 2023 12:00pm - 01:00 pm goo.gle/techtalksforedu with headshot of Pankaj Rai GDE - Android, Firebase, Machine Learning

Add Machine Learning to your Android App by ML GDE Pankaj Rai (India) at Tech Talks for Educators was a session on on-device ML and how to add ML capabilities to Android apps such as object detection and gesture detection. He explained capabilities of ML Kit, MediaPipe, TF Lite and how to use these tools. 700+ people registered for his talk.

In MediaPipe with a bit of Bard at I/O Extended Singapore 2023, ML GDE Martin Andrews (Singapore) shared how MediaPipe fits into the ecosystem, and showed 4 different demonstrations of MediaPipe functionality: audio classification, facial landmarks, interactive segmentation, and text classification.

Adding ML to our apps with Google ML Kit and MediaPipe by ML GDE Juan Guillermo Gomez Torres (Bolivia) introduced ML Kit & MediaPipe, and the benefits of on-device ML. In Startup Academy México (Google for Startups), he shared how to increase the value for clients with ML and MediaPipe.


LLM

Introduction to Google's PaLM 2 API by ML GDE Hannes Hapke (United States) introduced how to use PaLM2 and summarized major advantages of it. His another article The role of ML Engineering in the time of GPT-4 & PaLM 2 explains the role of ML experts in finding the right balance and alignment among stakeholders to optimally navigate the opportunities and challenges posed by this emerging technology. He did presentations under the same title at North America Connect 2023 and the GDG Portland event.

Image of a cellphone with ChatBard on the display in front of a computer display with Firebase PaLM in Cloud Firestore

ChatBard : An Intelligent Customer Service Center App by ML GDE Ruqiya Bin Safi (Saudi Arabia) is an intelligent customer service center app powered by generative AI and LLMs using PaLM2 APIs.

Bard can now code and put that code in Colab for you by ML GDE Sam Witteveen (Singapore) showed how Bard makes code. He runs a Youtube channel exploring ML and AI, with playlists such as Generative AI, Paper Reviews, LLMs, and LangChain.

Google’s Bard Can Write Code by ML GDE Bhavesh Bhatt (India) shows the coding capabilities of Bard, how to create a 2048 game with it, and how to add some basic features to the game. He also uploaded videos about LangChain in a playlist and introduced Google Cloud’s new course on Generative AI in this video.

Screengrab of GDG Deep Learning Course Attention Mechanisms and Transformers led by Ruqiya Bin Safi ML GDE & WTM Ambassador, @Ru0Sa

Attention Mechanisms and Transformers by GDG Cloud Saudi talked about Attention and Transformer in NLP and ML GDE Ruqiya Bin Safi (Saudi Arabia) participated as a speaker. Another event, Hands-on with the PaLM2 API to create smart apps(Jeddah) explored what LLMs, PaLM2, and Bard are, how to use PaLM2 API, and how to create smart apps using PaLM2 API.

Hands-on with Generative AI: Google I/O Extended [Virtual] by ML GDE Henry Ruiz (United States) and Web GDE Rabimba Karanjai (United States) was a workshop on generative AI showing hands-on demons of how to get started using tools such as PaLM API, Hugging Face Transformers, and LangChain framework.

Generative AI with Google PaLM and MakerSuite by ML GDE Kuan Hoong (Malaysia) at Google I/O Extended George Town 2023 was a talk about LLMs with Google PaLM and MakerSuite. The event hosted by GDG George Town and also included ML topics such as LLMs, responsible AI, and MLOps.

Intor to Gen AI with PaLM API and MakerSuite led by GUS Luis Gustavo and Tensorflow User Group Sao Paolo

Intro to Gen AI with PaLM API and MakerSuite by TFUG São Paulo was for people who want to learn generative AI and how Google tools can help with adoption and value creation. They covered how to start prototyping Gen AI ideas with MakerSuite and how to access advanced features of PaLM2 and PaLM API. The group also hosted Opening Pandora's box: Understanding the paper that revolutionized the field of NLP (video) and ML GDE Pedro Gengo (Brazil) and ML GDE Vinicius Caridá (Brazil) shared the secret behind the famous LLM and other Gen AI models.The group members studied Attention Is All You Need paper together and learned the full potential that the technology can offer.

Language models which PaLM can speak, see, move, and understand by GDG Cloud Taipei was for those who want to understand the concept and application of PaLM. ML GED Jerry Wu (Taiwan) shared the PaLM’s main characteristics, functions, and etc.

Flow chart illustrating flexible serving structure of stable diffusion

Serving With TF and GKE: Stable Diffusion by ML GDE Chansung Park (Korea) and ML GDE Sayak Paul (India) discusses how TF Serving and Kubernetes Engine can serve a system with online deployment. They broke down Stable Diffusion into main components and how they influence the subsequent consideration for deployment. Then they also covered the deployment-specific bits such as TF Serving deployment and k8s cluster configuration.

TFX + W&B Integration by ML GDE Chansung Park (Korea) shows how KerasTuner can be used with W&B’s experiment tracking feature within the TFX Tuner component. He developed a custom TFX component to push a full-trained model to the W&B Artifact store and publish a working application on Hugging Face Space with the current version of the model. Also, his talk titled, ML Infra and High Level Framework in Google Cloud Platform, delivered what MLOps is, why it is hard, why cloud + TFX is a good starter, and how TFX is seamlessly integrated with Vertex AI and Dataflow. He shared use cases from the past projects that he and ML GDE Sayak Paul (India) have done in the last 2 years.

Open and Collaborative MLOps by ML GDE Sayak Paul (India) was a talk about why openness and collaboration are two important aspects of MLOps. He gave an overview of Hugging Face Hub and how it integrates well with TFX to promote openness and collaboration in MLOps workflows.


ML Research

Paper review: PaLM 2 Technical Report by ML GDE Grigory Sapunov (UK) looked into the details of PaLM2 and the paper. He shares reviews of papers related to Google and DeepMind through his social channels and here are some of them: Model evaluation for extreme risks (paper), Faster sorting algorithms discovered using deep reinforcement learning (paper), Power-seeking can be probable and predictive for trained agents (paper).

Learning JAX in 2023: Part 3 — A Step-by-Step Guide to Training Your First Machine Learning Model with JAX by ML GDE Aritra Roy Gosthipaty (India) and ML GDE Ritwik Raha (India) shows how JAX can train linear and nonlinear regression models and the usage of PyTrees library to train a multilayer perceptron model. In addition, at May 2023 Meetup hosted by TFUG Mumbai, they gave a talk titled Decoding End to End Object Detection with Transformers and covered the architecture of the mode and the various components that led to DETR’s inception.

20 steps to train a deployed version of the GPT model on TPU by ML GDE Jerry Wu (Taiwan) shared how to use JAX and TPU to train and infer Chinese question-answering data.

Photo of the audience from the back of the room at Developer Space @Google Singapore during Multimodal Transformers - Custom LLMs, ViTs & BLIPs

Multimodal Transformers - Custom LLMs, ViTs & BLIPs by TFUG Singapore looked at what models, systems, and techniques have come out recently related to multimodal tasks. ML GDE Sam Witteveen (Singapore) looked into various multimodal models and systems and how you can build your own with the PaLM2 Model. In June, this group invited Blaise Agüera y Arcas (VP and Fellow at Google Research) and shared the Cerebra project and the research going on at Google DeepMind including the current and future developments in generative AI and emerging trends.


TensorFlow

Training a recommendation model with dynamic embeddings by ML GDE Thushan Ganegedara (Australia) explains how to build a movie recommender model by leveraging TensorFlow Recommenders (TFRS) and TensorFlow Recommenders Addons (TFRA). The primary focus was to show how the dynamic embeddings provided in the TFRA library can be used to dynamically grow and shrink the size of the embedding tables in the recommendation setting.

Screengrab of a tweet by Mathis Hammel showcasing his talk, 'How I built the most efficient deepfake detector in the world for $100'

How I built the most efficient deepfake detector in the world for $100 by ML GDE Mathis Hammel (France) was a talk exploring a method to detect images generated via ThisPersonDoesNotExist.com and even a way to know the exact time the photo was produced. Plus, his Twitter thread, OSINT Investigation on LinkedIn, investigated a network of fake companies on LinkedIn. He used a homemade tool based on a TensorFlow model and hosted it on Google Cloud. Technical explanations of generative neural networks were also included. More than 701K people viewed this thread and it got 1200+ RTs and 3100+ Likes.

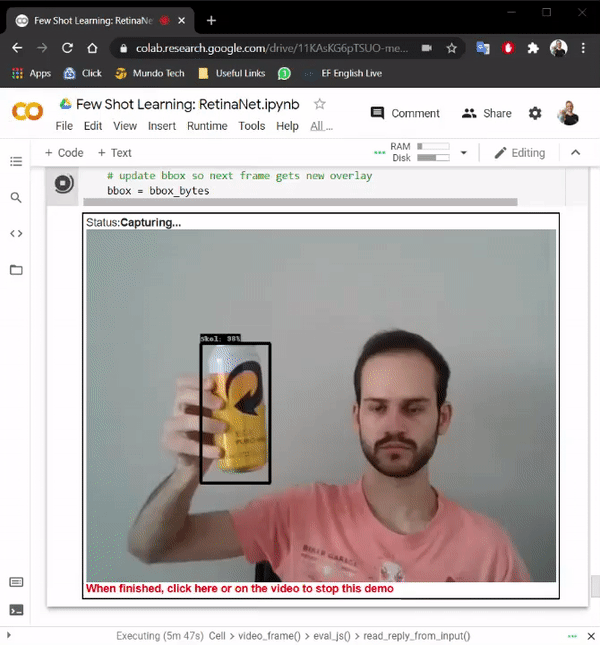
Screengrab of Few-shot learning: Creating a real-time object detection using TensorFlow and python by ML GDE Hugo Zanini

Few-shot learning: Creating a real-time object detection using TensorFlow and Python by ML GDE Hugo Zanini (Brazil) shows how to take pictures of an object using a webcam, label the images, and train a few-shot learning model to run in real-time. Also, his article, Custom YOLOv7 Object Detection with TensorFlow.js explains how he trained a custom YOLOv7 model to run it directly in the browser in real time and offline with TensorFlow.js.

The Lord of the Words Transformation of a Sequence Encoder/Decoder Attention

The Lord of the Words : The Return of the experiments with DVC (slides) by ML GDE Gema Parreno Piqueras (Spain) was a talk explaining Transformers in the neural machine learning scenario, and how to use Tensorflow and DVC. In the project, she used Tensorflow Datasets translation catalog to load data from various languages, and TensorFlow Transformers library to train several models.

Accelerate your TensorFlow models with XLA (slides) and Ship faster TensorFlow models with XLA by ML GDE Sayak Paul (India) shared how to accelerate TensorFlow models with XLA in Cloud Community Days Kolkata 2023 and Cloud Community Days Pune 2023.

Setup of NVIDIA Merlin and Tensorflow for Recommendation Models by ML GDE Rubens Zimbres (Brazil) presented a review of recommendation algorithms as well as the Two Towers algorithm, and setup of NVIDIA Merlin on premises and on Vertex AI.


Cloud

AutoML pipeline for tabular data on VertexAI in Go by ML GDE Paolo Galeone (Italy) delved into the development and deployment of tabular models using VertexAI and AutoML with Go, showcasing the actual Go code and sharing insights gained through trial & error and extensive Google research to overcome documentation limitations.

Search engine architecture

Beyond images: searching information in videos using AI (slides) by ML GDE Pedro Gengo (Brazil) and ML GDE Vinicius Caridá (Brazil) showed how to create a search engine where you can search for information in videos. They presented an architecture where they transcribe the audio and caption the frames, convert this text into embeddings, and save them in a vector DB to be able to search given a user query.

The secret sauce to creating amazing ML experiences for developers by ML GDE Gant Laborde (United States) was a podcast sharing his “aha” moment, 20 years of experience in ML, and the secret to creating enjoyable and meaningful experiences for developers.

What's inside Google’s Generative AI Studio? by ML GDE Gad Benram (Portugal) shared the preview of the new features and what you can expect from it. Additionally, in How to pitch Vertex AI in 2023, he shared the six simple and honest sales pitch points for Google Cloud representatives on how to convince customers that Vertex AI is the right platform.

In How to build a conversational AI Augmented Reality Experience with Sachin Kumar, ML GDE Sachin Kumar (Qatar) talked about how to build an AR app combining multiple technologies like Google Cloud AI, Unity, and etc. The session walked through the step-by-step process of building the app from scratch.

Machine Learning on Google Cloud Platform led by Nitin Tiwari, Google Developer Expert - Machine Learning, Software Engineer @LTMIMindtree

Machine Learning on Google Cloud Platform by ML GDE Nitin Tiwari (India) was a mentoring aiming to provide students with an in-depth understanding of the processes involved in training an ML model and deploying it using GCP. In Building robust ML solutions with TensorFlow and GCP, he shared how to leverage the capabilities of GCP and TensorFlow for ML solutions and deploy custom ML models.

Data to AI on Google cloud: Auto ML, Gen AI, and more by TFUG Prayagraj educated students on how to leverage Google Cloud’s advanced AI technologies, including AutoML and generative AI.

PJRT: Simplifying ML Hardware and Framework Integration

Infrastructure fragmentation in Machine Learning (ML) across frameworks, compilers, and runtimes makes developing new hardware and toolchains challenging. This inhibits the industry’s ability to quickly productionize ML-driven advancements. To simplify the growing complexity of ML workload execution across hardware and frameworks, we are excited to introduce PJRT and open source it as part of the recently available OpenXLA Project.

PJRT (used in conjunction with OpenXLA’s StableHLO) provides a hardware- and framework-independent interface for compilers and runtimes. It simplifies the integration of hardware with frameworks, accelerating framework coverage for the hardware, and thus hardware targetability for workload execution.

PJRT is the primary interface for TensorFlow and JAX and fully supported for PyTorch, and is well integrated with the OpenXLA ecosystem to execute workloads on TPU, GPU, and CPU. It is also the default runtime execution path for most of Google’s internal production workloads. The toolchain-independent architecture of PJRT allows it to be leveraged by any hardware, framework, or compiler, with extensibility for unique features. With this open-source release, we're excited to allow anyone to begin leveraging PJRT for their own devices.

If you’re developing an ML hardware accelerator or developing your own compiler and runtime, check out the PJRT source code on GitHub and sign up for the OpenXLA mailing list to quickly bootstrap your work.

Vision: Simplifying ML Hardware and Framework Integration

We are entering a world of ambient experiences where intelligent apps and devices surround us, from edge to the cloud, in a range of environments and scales. ML workload execution currently supports a combinatorial matrix of hardware, frameworks, and workflows, mostly through tight vertical integrations. Examples of such vertical integrations include specific kernels for TPU versus GPU, specific toolchains to train and serve in TensorFlow versus PyTorch. These bespoke 1:1 integrations are perfectly valid solutions but promote lock-in, inhibit innovation, and are expensive to maintain. This problem of a fragmented software stack is compounded over time as different computing hardware needs to be supported.

A variety of ML hardware exists today and hardware diversity is expected to increase in the future. ML users have options and they want to exercise them seamlessly: users want to train a large language model (LLM) on TPU in the Cloud, batch infer on GPU or even CPU, distill, quantize, and finally serve them on mobile processors. Our goal is to solve the challenge of making ML workloads portable across hardware by making it easy to integrate the hardware into the ML infrastructure (framework, compiler, runtime).

Portability: Seamless Execution

The workflow to enable this vision with PJRT is as follows (shown in Figure 1):

  1. The hardware-specific compiler and runtime provider implement the PJRT API, package it as a plugin containing the compiler and runtime hooks, and register it with the frameworks. The implementation can be opaque to the frameworks.
  2. The frameworks discover and load one or multiple PJRT plugins as dynamic libraries targeting the hardware on which to execute the workload.
  3. That’s it! Execute the workload from the framework onto the target hardware.

The PJRT API will be backward compatible. The plugin would not need to change often and would be able to do version-checking for features.

Diagram of PJRT architecture
Figure 1: To target specific hardware, provide an implementation of the PJRT API to package a compiler and runtime plugin that can be called by the framework.

Cohesive Ecosystem

As a foundational pillar of the OpenXLA Project, PJRT is well-integrated with projects within the OpenXLA Project including StableHLO and the OpenXLA compilers (XLA, IREE). It is the primary interface for TensorFlow and JAX and fully supported for PyTorch through PyTorch/XLA. It provides the hardware interface layer in solving the combinatorial framework x hardware ML infrastructure fragmentation (see Figure 2).

Diagram of PJRT hardware interface layer
Figure 2: PJRT provides the hardware interface layer in solving the combinatorial framework x hardware ML infrastructure fragmentation, well-integrated with OpenXLA.

Toolchain Independent

PJRT is hardware and framework independent. With framework integration through the self-contained IR StableHLO, PJRT is not coupled with a specific compiler, and can be used outside of the OpenXLA ecosystem, including with other proprietary compilers. The public availability and toolchain-independent architecture allows it to be used by any hardware, framework or compiler, with extensibility for unique features. If you are developing an ML hardware accelerator, compiler, or runtime targeting any hardware, or converging siloed toolchains to solve infrastructure fragmentation, PJRT can minimize bespoke hardware and framework integration, providing greater coverage and improving time-to-market at lower development cost.

Driving Impact with Collaboration

Industry partners such as Intel and others have already adopted PJRT.

Intel

Intel is leveraging PJRT in Intel® Extension for TensorFlow to provide the Intel GPU backend for TensorFlow and JAX. This implementation is based on the PJRT plugin mechanism (see RFC). Check out how this greatly simplifies the framework and hardware integration with this example of executing a JAX program on Intel GPU.

"At Intel, we share Google's vision of modular interfaces to make integration easier and enable faster, framework-independent development. Similar in design to the PluggableDevice mechanism, PJRT is a pluggable interface that allows us to easily compile and execute XLA's High Level Operations on Intel devices. Its simple design allowed us to quickly integrate it into our systems and start running JAX workloads on Intel® GPUs within just a few months. PJRT enables us to more efficiently deliver hardware acceleration and oneAPI-powered AI software optimizations to developers using a wide range of AI Frameworks." - Wei Li, VP and GM, Artificial Intelligence and Analytics, Intel.

Technology Leader

We’re also working with a technology leader to leverage PJRT to provide the backend targeting their proprietary processor for JAX. More details on this to follow soon.

Get Involved

PJRT is available on GitHub: source code for the API and a reference openxla-pjrt-plugin, and integration guides. If you develop ML frameworks, compilers, or runtimes, or are interested in improving portability of workloads across hardware, we want your feedback. We encourage you to contribute code, design ideas, and feature suggestions. We also invite you to join the OpenXLA mailing list to stay updated with the latest product and community announcements and to help shape the future of an interoperable ML infrastructure.

Acknowledgements

Allen Hutchison, Andrew Leaver, Chuanhao Zhuge, Jack Cao, Jacques Pienaar, Jieying Luo, Penporn Koanantakool, Peter Hawkins, Robert Hundt, Russell Power, Sagarika Chalasani, Skye Wanderman-Milne, Stella Laurenzo, Will Cromar, Xiao Yu.

By Aman Verma, Product Manager, Machine Learning Infrastructure

Machine Learning Communities: Q1 ‘23 highlights and achievements

Posted by Nari Yoon, Bitnoori Keum, Hee Jung, DevRel Community Manager / Soonson Kwon, DevRel Program Manager

Let’s explore highlights and accomplishments of vast Google Machine Learning communities over the first quarter of 2023. We are enthusiastic and grateful about all the activities by the global network of ML communities. Here are the highlights!



ML Campaigns



ML Community Sprint

ML Community Sprint is a campaign, a collaborative attempt bridging ML GDEs with Googlers to produce relevant content for the broader ML community. Throughout Feb and Mar, MediaPipe/TF Recommendation Sprint was carried out and 5 projects were completed.


ML Olympiad 2023
I'm hosting a competiton ML Olympiad 2023 #MLOlympiad

ML Olympiad is an associated Kaggle Community Competitions hosted by ML GDE, TFUG, 3rd-party ML communities, supported by Google Developers. The second, ML Olympiad 2023 has wrapped up successfully with 17 competitions and 300+ participants addressing important issues of our time - diversity, environments, etc. Competition highlights include Breast Cancer Diagnosis, Water Quality Prediction, Detect ChatGpt answers, Ensure healthy lives, etc. Thank you all for participating in ML Olympiad 2023!

Also, “ML Paper Reading Clubs” (GalsenAI and TFUG Dhaka), “ML Math Clubs” (TFUG Hajipur and TFUG Dhaka) and “ML Study Jams” (TFUG Bauchi) were hosted by ML communities around the world.


Community Highlights



Keras
Screen shot of Fine-tuning Stable Diffusion using Keras

Various ways of serving Stable Diffusion by ML GDE Chansung Park (Korea) and ML GDE Sayak Paul (India) shares how to deploy Stable Diffusion with TF Serving, Hugging Face Endpoint, and FastAPI. Their other project Fine-tuning Stable Diffusion using Keras provides how to fine-tune the image encoder of Stable Diffusion on a custom dataset consisting of image-caption pairs.

Serving TensorFlow models with TFServing by ML GDE Dimitre Oliveira (Brazil) is a tutorial explaining how to create a simple MobileNet using the Keras API and how to serve it with TF Serving.

Fine-tuning the multilingual T5 model from Huggingface with Keras by ML GDE Radostin Cholakov (Bulgaria) shows a minimalistic approach for training text generation architectures from Hugging Face with TensorFlow and Keras as the backend.


Image showing a range of low-lit pictures enhanced incljuding inference time and ther metrics

Lighting up Images in the Deep Learning Era by ML GDE Soumik Rakshit (India), ML GDE Saurav Maheshkar (UK), ML GDE Aritra Roy Gosthipaty (India), and Samarendra Dash explores deep learning techniques for low-light image enhancement. The article also talks about a library, Restorers, providing TensorFlow and Keras implementations of SoTA image and video restoration models for tasks such as low-light enhancement, denoising, deblurring, super-resolution, etc.

How to Use Cosine Decay Learning Rate Scheduler in Keras? by ML GDE Ayush Thakur (India) introduces how to correctly use the cosine-decay learning rate scheduler using Keras API.


Screen shot of Implementation of DreamBooth using KerasCV and TensorFlow

Implementation of DreamBooth using KerasCV and TensorFlow (Keras.io tutorial) by ML GDE Sayak Paul (India) and ML GDE Chansung Park (Korea) demonstrates DreamBooth technique to fine-tune Stable Diffusion in KerasCV and TensorFlow. Training code, inference notebooks, a Keras.io tutorial, and more are in the repository. Sayak also shared his story, [ML Story] DreamBoothing Your Way into Greatness on the GDE blog.

Focal Modulation: A replacement for Self-Attention by ML GDE Aritra Roy Gosthipaty (India) shares a Keras implementation of the paper. Usha Rengaraju (India) shared Keras Implementation of NeurIPS 2021 paper, Augmented Shortcuts for Vision Transformers.

Images classification with TensorFlow & Keras (video) by TFUG Abidjan explained how to define an ML model that can classify images according to the category using a CNN.

Hands-on Workshop on KerasNLP by GDG NYC, GDG Hoboken, and Stevens Institute of Technology shared how to use pre-trained Transformers (including BERT) to classify text, fine-tune it on custom data, and build a Transformer from scratch.


On-device ML

Stable diffusion example in an android application — Part 1 & Part 2 by ML GDE George Soloupis (Greece) demonstrates how to deploy a Stable Diffusion pipeline inside an Android app.

AI for Art and Design by ML GDE Margaret Maynard-Reid (United States) delivered a brief overview of how AI can be used to assist and inspire artists & designers in their creative space. She also shared a few use cases of on-device ML for creating artistic Android apps.


ML Engineering (MLOps)
Overall system architecture of End-to-End Pipeline for Segmentation with TFX, Google Cloud, and Hugging Face

End-to-End Pipeline for Segmentation with TFX, Google Cloud, and Hugging Face by ML GDE Sayak Paul (India) and ML GDE Chansung Park (Korea) discussed the crucial details of building an end-to-end ML pipeline for Semantic Segmentation tasks with TFX and various Google Cloud services such as Dataflow, Vertex Pipelines, Vertex Training, and Vertex Endpoint. The pipeline uses a custom TFX component that is integrated with Hugging Face Hub - HFPusher.

Extend your TFX pipeline with TFX-Addons by ML GDE Hannes Hapke (United States) explains how you can use the TFX-Addons components or examples.



Textual Inversion Pipeline architecture

Textual Inversion Pipeline for Stable Diffusion by ML GDE Chansung Park (Korea) demonstrates how to manage multiple models and their prototype applications of fine-tuned Stable Diffusion on new concepts by Textual Inversion.

Running a Stable Diffusion Cluster on GCP with tensorflow-serving (Part 1 | Part 2) by ML GDE Thushan Ganegedara (Australia) explains how to set up a GKE cluster, how to use Terraform to set up and manage infrastructure on GCP, and how to deploy a model on GKE using TF Serving.


Photo of Googler Joinal Ahmed giving a talk at TFUG Bangalore

Scalability of ML Applications by TFUG Bangalore focused on the challenges and solutions related to building and deploying ML applications at scale. Googler Joinal Ahmed gave a talk entitled Scaling Large Language Model training and deployments.

Discovering and Building Applications with Stable Diffusion by TFUG São Paulo was for people who are interested in Stable Diffusion. They shared how Stable Diffusion works and showed a complete version created using Google Colab and Vertex AI in production.


Responsible AI
Thumbnail image for Between the Brackets Fairness & Ethics in AI: Perspectives from Journalism, Medicine and Translation

In Fairness & Ethics In AI: From Journalism, Medicine and Translation, ML GDE Samuel Marks (United States) discussed responsible AI.

In The new age of AI: A Convo with Google Brain, ML GDE Vikram Tiwari (United States) discussed responsible AI, open-source vs. closed-source, and the future of LLMs.

Responsible IA Toolkit (video) by ML GDE Lesly Zerna (Bolivia) and Google DSC UNI was a meetup to discuss ethical and sustainable approaches to AI development. Lesly shared about the “ethic” side of building AI products as well as learning about “Responsible AI from Google”, PAIR guidebook, and other experiences to build AI.

Women in AI/ML at Google NYC by GDG NYC discussed hot topics, including LLMs and generative AI. Googler Priya Chakraborty gave a talk entitled Privacy Protections for ML Models.


ML Research

Efficient Task-Oriented Dialogue Systems with Response Selection as an Auxiliary Task by ML GDE Radostin Cholakov (Bulgaria) showcases how, in a task-oriented setting, the T5-small language model can perform on par with existing systems relying on T5-base or even bigger models.

Learning JAX in 2023: Part 1 / Part 2 / Livestream video by ML GDE Aritra Roy Gosthipaty (India) and ML GDE Ritwik Raha (India) covered the power tools of JAX, namely grad, jit, vmap, pmap, and also discussed the nitty-gritty of randomness in JAX.


Screen grab from JAX Streams: Parallelism with Flax | Ep4 with David Cardozo and Cristian Garcia

In Deep Learning Mentoring MILA Quebec, ML GDE David Cardozo (Canada) did mentoring for M.Sc and Ph.D. students who have interests in JAX and MLOps. JAX Streams: Parallelism with Flax | EP4 by David and ML GDE Cristian Garcia (Columbia) explored Flax’s new APIs to support parallelism.

March Machine Learning Meetup hosted by TFUG Kolkata. Two sessions were delivered: 1) You don't know TensorFlow by ML GDE Sayak Paul (India) presented some under-appreciated and under-used features of TensorFlow. 2) A Guide to ML Workflows with JAX by ML GDE Aritra Roy Gosthipaty (India), ML GDE Soumik Rakshit (India), and ML GDE Ritwik Raha (India) delivered on how one could think of using JAX functional transformations for their ML workflows.

A paper review of PaLM-E: An Embodied Multimodal Language Model by ML GDE Grigory Sapunov (UK) explained the details of the model. He also shared his slide deck about NLP in 2022.

An annotated paper of On the importance of noise scheduling in Diffusion Models by ML GDE Aakash Nain (India) outlined the effects of noise schedule on the performance of diffusion models and strategies to get a better schedule for optimal performance.


TensorFlow

Three projects were awarded as TF Community Spotlight winners: 1) Semantic Segmentation model within ML pipeline by ML GDE Chansung Park (Korea), ML GDE Sayak Paul (India), and ML GDE Merve Noyan (France), 2) GatedTabTransformer in TensorFlow + TPU / in Flax by Usha Rengaraju, and 3) Real-time Object Detection in the browser with YOLOv7 and TF.JS by ML GDE Hugo Zanini (Brazil).

Building ranking models powered by multi-task learning with Merlin and TensorFlow by ML GDE Gabriel Moreira (Brazil) describes how to build TensorFlow models with Merlin for recommender systems using multi-task learning.


Transform your Web Apps with Machine Learning: Unleashing the Power of Open-Source Python Libraries like TensorFlow Hub & Gradio Bhjavesh Bhatt @_bhaveshbhatt

Building ML Powered Web Applications using TensorFlow Hub & Gradio (slide) by ML GDE Bhavesh Bhatt (India) demonstrated how to use TF Hub & Gradio to create a fully functional ML-powered web application. The presentation was held as part of an event called AI Evolution with TensorFlow, covering the fundamentals of ML & TF, hosted by TFUG Nashik.

create-tf-app (repository) by ML GDE Radostin Cholakov (Bulgaria) shows how to set up and maintain an ML project in Tensorflow with a single script.


Cloud

Creating scalable ML solutions to support big techs evolution (slide) by ML GDE Mikaeri Ohana (Brazil) shared how Google can help big techs to generate impact through ML with scalable solutions.

Search of Brazilian Laws using Dialogflow CX and Matching Engine by ML GDE Rubens Zimbres (Brazil) shows how to build a chatbot with Dialogflow CX and query a database of Brazilian laws by calling an endpoint in Cloud Run.


4x4 grid of sample results from Vintedois Diffusion model

Stable Diffusion Finetuning by ML GDE Pedro Gengo (Brazil) and ML GDE Piero Esposito (Brazil) is a fine-tuned Stable Diffusion 1.5 with more aesthetic images. They used Vertex AI with multiple GPUs to fine-tune it. It reached Hugging Face top 3 and more than 150K people downloaded and tested it.

Visual Blocks for ML: Accelerating machine learning prototyping with interactive tools

Posted by Ruofei Du, Interactive Perception & Graphics Lead, Google Augmented Reality, and Na Li, Tech Lead Manager, Google CoreML

Recent deep learning advances have enabled a plethora of high-performance, real-time multimedia applications based on machine learning (ML), such as human body segmentation for video and teleconferencing, depth estimation for 3D reconstruction, hand and body tracking for interaction, and audio processing for remote communication.

However, developing and iterating on these ML-based multimedia prototypes can be challenging and costly. It usually involves a cross-functional team of ML practitioners who fine-tune the models, evaluate robustness, characterize strengths and weaknesses, inspect performance in the end-use context, and develop the applications. Moreover, models are frequently updated and require repeated integration efforts before evaluation can occur, which makes the workflow ill-suited to design and experiment.

In “Rapsai: Accelerating Machine Learning Prototyping of Multimedia Applications through Visual Programming”, presented at CHI 2023, we describe a visual programming platform for rapid and iterative development of end-to-end ML-based multimedia applications. Visual Blocks for ML, formerly called Rapsai, provides a no-code graph building experience through its node-graph editor. Users can create and connect different components (nodes) to rapidly build an ML pipeline, and see the results in real-time without writing any code. We demonstrate how this platform enables a better model evaluation experience through interactive characterization and visualization of ML model performance and interactive data augmentation and comparison. Sign up to be notified when Visual Blocks for ML is publicly available.

Visual Blocks uses a node-graph editor that facilitates rapid prototyping of ML-based multimedia applications.


Formative study: Design goals for rapid ML prototyping

To better understand the challenges of existing rapid prototyping ML solutions (LIME, VAC-CNN, EnsembleMatrix), we conducted a formative study (i.e., the process of gathering feedback from potential users early in the design process of a technology product or system) using a conceptual mock-up interface. Study participants included seven computer vision researchers, audio ML researchers, and engineers across three ML teams.

The formative study used a conceptual mock-up interface to gather early insights.

Through this formative study, we identified six challenges commonly found in existing prototyping solutions:

  1. The input used to evaluate models typically differs from in-the-wild input with actual users in terms of resolution, aspect ratio, or sampling rate.
  2. Participants could not quickly and interactively alter the input data or tune the model.
  3. Researchers optimize the model with quantitative metrics on a fixed set of data, but real-world performance requires human reviewers to evaluate in the application context.
  4. It is difficult to compare versions of the model, and cumbersome to share the best version with other team members to try it.
  5. Once the model is selected, it can be time-consuming for a team to make a bespoke prototype that showcases the model.
  6. Ultimately, the model is just part of a larger real-time pipeline, in which participants desire to examine intermediate results to understand the bottleneck.

These identified challenges informed the development of the Visual Blocks system, which included six design goals: (1) develop a visual programming platform for rapidly building ML prototypes, (2) support real-time multimedia user input in-the-wild, (3) provide interactive data augmentation, (4) compare model outputs with side-by-side results, (5) share visualizations with minimum effort, and (6) provide off-the-shelf models and datasets.


Node-graph editor for visually programming ML pipelines

Visual Blocks is mainly written in JavaScript and leverages TensorFlow.js and TensorFlow Lite for ML capabilities and three.js for graphics rendering. The interface enables users to rapidly build and interact with ML models using three coordinated views: (1) a Nodes Library that contains over 30 nodes (e.g., Image Processing, Body Segmentation, Image Comparison) and a search bar for filtering, (2) a Node-graph Editor that allows users to build and adjust a multimedia pipeline by dragging and adding nodes from the Nodes Library, and (3) a Preview Panel that visualizes the pipeline’s input and output, alters the input and intermediate results, and visually compares different models.

The visual programming interface allows users to quickly develop and evaluate ML models by composing and previewing node-graphs with real-time results.


Iterative design, development, and evaluation of unique rapid prototyping capabilities

Over the last year, we’ve been iteratively designing and improving the Visual Blocks platform. Weekly feedback sessions with the three ML teams from the formative study showed appreciation for the platform’s unique capabilities and its potential to accelerate ML prototyping through:

  • Support for various types of input data (image, video, audio) and output modalities (graphics, sound).
  • A library of pre-trained ML models for common tasks (body segmentation, landmark detection, portrait depth estimation) and custom model import options.
  • Interactive data augmentation and manipulation with drag-and-drop operations and parameter sliders.
  • Side-by-side comparison of multiple models and inspection of their outputs at different stages of the pipeline.
  • Quick publishing and sharing of multimedia pipelines directly to the web.

Evaluation: Four case studies

To evaluate the usability and effectiveness of Visual Blocks, we conducted four case studies with 15 ML practitioners. They used the platform to prototype different multimedia applications: portrait depth with relighting effects, scene depth with visual effects, alpha matting for virtual conferences, and audio denoising for communication.

The system streamlining comparison of two Portrait Depth models, including customized visualization and effects.

With a short introduction and video tutorial, participants were able to quickly identify differences between the models and select a better model for their use case. We found that Visual Blocks helped facilitate rapid and deeper understanding of model benefits and trade-offs:

“It gives me intuition about which data augmentation operations that my model is more sensitive [to], then I can go back to my training pipeline, maybe increase the amount of data augmentation for those specific steps that are making my model more sensitive.” (Participant 13)
“It’s a fair amount of work to add some background noise, I have a script, but then every time I have to find that script and modify it. I’ve always done this in a one-off way. It’s simple but also very time consuming. This is very convenient.” (Participant 15)
The system allows researchers to compare multiple Portrait Depth models at different noise levels, helping ML practitioners identify the strengths and weaknesses of each.

In a post-hoc survey using a seven-point Likert scale, participants reported Visual Blocks to be more transparent about how it arrives at its final results than Colab (Visual Blocks 6.13 ± 0.88 vs. Colab 5.0 ± 0.88, 𝑝 < .005) and more collaborative with users to come up with the outputs (Visual Blocks 5.73 ± 1.23 vs. Colab 4.15 ± 1.43, 𝑝 < .005). Although Colab assisted users in thinking through the task and controlling the pipeline more effectively through programming, Users reported that they were able to complete tasks in Visual Blocks in just a few minutes that could normally take up to an hour or more. For example, after watching a 4-minute tutorial video, all participants were able to build a custom pipeline in Visual Blocks from scratch within 15 minutes (10.72 ± 2.14). Participants usually spent less than five minutes (3.98 ± 1.95) getting the initial results, then were trying out different input and output for the pipeline.

User ratings between Rapsai (initial prototype of Visual Blocks) and Colab across five dimensions.

More results in our paper showed that Visual Blocks helped participants accelerate their workflow, make more informed decisions about model selection and tuning, analyze strengths and weaknesses of different models, and holistically evaluate model behavior with real-world input.


Conclusions and future directions

Visual Blocks lowers development barriers for ML-based multimedia applications. It empowers users to experiment without worrying about coding or technical details. It also facilitates collaboration between designers and developers by providing a common language for describing ML pipelines. In the future, we plan to open this framework up for the community to contribute their own nodes and integrate it into many different platforms. We expect visual programming for machine learning to be a common interface across ML tooling going forward.


Acknowledgements

This work is a collaboration across multiple teams at Google. Key contributors to the project include Ruofei Du, Na Li, Jing Jin, Michelle Carney, Xiuxiu Yuan, Kristen Wright, Mark Sherwood, Jason Mayes, Lin Chen, Jun Jiang, Scott Miles, Maria Kleiner, Yinda Zhang, Anuva Kulkarni, Xingyu "Bruce" Liu, Ahmed Sabie, Sergio Escolano, Abhishek Kar, Ping Yu, Ram Iyengar, Adarsh Kowdle, and Alex Olwal.

We would like to extend our thanks to Jun Zhang and Satya Amarapalli for a few early-stage prototypes, and Sarah Heimlich for serving as a 20% program manager, Sean Fanello, Danhang Tang, Stephanie Debats, Walter Korman, Anne Menini, Joe Moran, Eric Turner, and Shahram Izadi for providing initial feedback for the manuscript and the blog post. We would also like to thank our CHI 2023 reviewers for their insightful feedback.

Source: Google AI Blog


How students are making an impact on mental health through technology

Posted by Laura Cincera, Program Manager Google Developer Student Clubs Europe

Mental health remains one of the most neglected areas of healthcare worldwide, with nearly 1 billion people currently living with a mental health condition that requires support. But what if there was a way to make mental health care more accessible and tailored to individual needs?

The Google Developer Student Clubs Solution Challenge aims to inspire and empower university students to tackle our most pressing challenges - like mental health. The Solution Challenge is an annual opportunity to turn visionary ideas into reality and make a real-world impact using the United Nations' 17 Sustainable Development Goals as a blueprint for action. Students from all over the world work together and apply their skills to create innovative solutions using Google technology, creativity and the power of community.

One of last year’s top Solution Challenge proposals, Xtrinsic, was a cooperation between two communities of student leaders - GDSC Freiburg in Germany and GDSC Kyiv in Ukraine. The team developed an innovative mental health research and therapy application that adapts to users' personal habits and needs providing effective support at scale.

The team behind Xtrinsic includes Alexander Monneret, Chikordili Fabian Okeke, Emma Rein, and Vandysh Kateryna, who come from different backgrounds but share a common mission to improve mental health research and therapy.

Using a wearable device and TensorFlow, Xtrinsic helps users manage their symptoms by providing customized behavioral suggestions based on their physiological signs. It acts as an intervention tool for mental health issues such as nightmares, panic attacks, and anxiety and adapts the user's environment to their specific needs - which is essential for effective interventions. For example, if the user experiences a panic attack, the app detects the physiological signs using a smartwatch and a machine learning model, and triggers appropriate action, such as playing relaxing sounds, changing the room light to blue, or starting a guided breathing exercise. The solution was built using several Google technologies, including Android, Assistant/Actions on Google, Firebase, Flutter, Google Cloud, TensorFlow, WearOS, DialogFlow, and Google Health Services.

The team behind Xtrinsic is diverse. Alexander, Chikordili, Emma and Vandysh come from different backgrounds but share a passion for AI and how it can be leveraged to improve the lives of many. They all recognize the importance of shedding awareness on mental health and creating a supportive culture that is free from stigma. Their personal experiences in conflict areas, such as Syria and Ukraine inspired them to develop the application.

Solution Challenge Google Developer Student Clubs Xtrinsic project For mental health research and therapy GDSC Ukraine and Germany

Xtrinsic was recognized as one of the Top 3 winning teams in the 2022 Google Solution Challenge for its innovative approach to mental health research and therapy. The team has since supported several other social impact initiatives - helping grow the network of entrepreneurs and community leaders in Europe and beyond.

Google Developer Student Clubs Help students grow and build solutions

Learn more about Google Developer Student Clubs

If you feel inspired to make a positive change through technology, submit your project to Solution Challenge 2023 here. And if you’re passionate about technology and are ready to use your skills to help your local community, then consider becoming a Google Developer Student Clubs Lead!

We encourage all interested university students to apply here and submit their applications as soon as possible. The applications in Europe, India, North America and MENA are currently open.

Learn more about Google Developer Student Clubs here.