Tag Archives: deep learning

Magika: AI powered fast and efficient file type identification

Today we are open-sourcing Magika, Google’s AI-powered file-type identification system, to help others accurately detect binary and textual file types. Under the hood, Magika employs a custom, highly optimized deep-learning model, enabling precise file identification within milliseconds, even when running on a CPU.

Magika command line tool used to recognize a identify the type of a diverse set of files

You can try the Magika web demo today, or install it as a Python library and standalone command line tool (output is showcased above) by using the standard command line pip install magika.

Why identifying file type is difficult

Since the early days of computing, accurately detecting file types has been crucial in determining how to process files. Linux comes equipped with libmagic and the file utility, which have served as the de facto standard for file type identification for over 50 years. Today web browsers, code editors, and countless other software rely on file-type detection to decide how to properly render a file. For example, modern code editors use file-type detection to choose which syntax coloring scheme to use as the developer starts typing in a new file.

Accurate file-type detection is a notoriously difficult problem because each file format has a different structure, or no structure at all. This is particularly challenging for textual formats and programming languages as they have very similar constructs. So far, libmagic and most other file-type-identification software have been relying on a handcrafted collection of heuristics and custom rules to detect each file format.

This manual approach is both time consuming and error prone as it is hard for humans to create generalized rules by hand. In particular for security applications, creating dependable detection is especially challenging as attackers are constantly attempting to confuse detection with adversarially-crafted payloads.

To address this issue and provide fast and accurate file-type detection we researched and developed Magika, a new AI powered file type detector. Under the hood, Magika uses a custom, highly optimized deep-learning model designed and trained using Keras that only weighs about 1MB. At inference time Magika uses Onnx as an inference engine to ensure files are identified in a matter of milliseconds, almost as fast as a non-AI tool even on CPU.

Magika Performance

Magika detection quality compared to other tools on our 1M files benchmark

Performance wise, Magika, thanks to its AI model and large training dataset, is able to outperform other existing tools by about 20% when evaluated on a 1M files benchmark that encompasses over 100 file types. Breaking down by file type, as reported in the table below, we see even greater performance gains on textual files, including code files and configuration files that other tools can struggle with.

Table showing various file type identification tools performance for a selection of the file types included in our benchmark

Various file type identification tools performance for a selection of the file types included in our benchmark - n/a indicates the tool doesn’t detect the given file type.

Magika at Google

Internally, Magika is used at scale to help improve Google users’ safety by routing Gmail, Drive, and Safe Browsing files to the proper security and content policy scanners. Looking at a weekly average of hundreds of billions of files reveals that Magika improves file type identification accuracy by 50% compared to our previous system that relied on handcrafted rules. In particular, this increase in accuracy allows us to scan 11% more files with our specialized malicious AI document scanners and reduce the number of unidentified files to 3%.

The upcoming integration of Magika with VirusTotal will complement the platform's existing Code Insight functionality, which employs Google's generative AI to analyze and detect malicious code. Magika will act as a pre-filter before files are analyzed by Code Insight, improving the platform’s efficiency and accuracy. This integration, due to VirusTotal’s collaborative nature, directly contributes to the global cybersecurity ecosystem, fostering a safer digital environment.

Open Sourcing Magika

By open-sourcing Magika, we aim to help other software improve their file identification accuracy and offer researchers a reliable method for identifying file types at scale.

Magika code and model are freely available starting today in Github under the Apache2 License. Magika can also quickly be installed as a standalone utility and python library via the pypi package manager by simply typing pip install magika with no GPU required. We also have an experimental npm package if you would like to use the TFJS version.

To learn more about how to use it, please refer to Magika documentation site.

Acknowledgements

Magika would not have been possible without the help of many people including: Ange Albertini, Loua Farah, Francois Galilee, Giancarlo Metitieri, Luca Invernizzi, Young Maeng, Alex Petit-Bianco , David Tao, Kurt Thomas, Amanda Walker

By Elie Bursztein – Cybersecurity AI Technical and Research Lead and Yanick Fratantonio – Cybersecurity Research Scientist

Source: Google Open Source Blog

Magika: AI powered fast and efficient file type identification

Magika command line tool used to recognize a identify the type of a diverse set of files

You can try the Magika web demo today, or install it as a Python library and standalone command line tool (output is showcased above) by using the standard command line pip install magika.

Why identifying file type is difficult

Magika Performance

Magika detection quality compared to other tools on our 1M files benchmark

Various file type identification tools performance for a selection of the file types included in our benchmark - n/a indicates the tool doesn’t detect the given file type.

Magika at Google

Open Sourcing Magika

By open-sourcing Magika, we aim to help other software improve their file identification accuracy and offer researchers a reliable method for identifying file types at scale.

To learn more about how to use it, please refer to Magika documentation site.

Acknowledgements

By Elie Bursztein – Cybersecurity AI Technical and Research Lead and Yanick Fratantonio – Cybersecurity Research Scientist

Source: Google Open Source Blog

Learning the importance of training data under concept drift

Posted by Nishant Jain, Pre-doctoral Researcher, and Pradeep Shenoy, Research Scientist, Google Research

The constantly changing nature of the world around us poses a significant challenge for the development of AI models. Often, models are trained on longitudinal data with the hope that the training data used will accurately represent inputs the model may receive in the future. More generally, the default assumption that all training data are equally relevant often breaks in practice. For example, the figure below shows images from the CLEAR nonstationary learning benchmark, and it illustrates how visual features of objects evolve significantly over a 10 year span (a phenomenon we refer to as slow concept drift), posing a challenge for object categorization models.

Sample images from the CLEAR benchmark. (Adapted from Lin et al.)

Alternative approaches, such as online and continual learning, repeatedly update a model with small amounts of recent data in order to keep it current. This implicitly prioritizes recent data, as the learnings from past data are gradually erased by subsequent updates. However in the real world, different kinds of information lose relevance at different rates, so there are two key issues: 1) By design they focus exclusively on the most recent data and lose any signal from older data that is erased. 2) Contributions from data instances decay uniformly over time irrespective of the contents of the data.

In our recent work, “Instance-Conditional Timescales of Decay for Non-Stationary Learning”, we propose to assign each instance an importance score during training in order to maximize model performance on future data. To accomplish this, we employ an auxiliary model that produces these scores using the training instance as well as its age. This model is jointly learned with the primary model. We address both the above challenges and achieve significant gains over other robust learning methods on a range of benchmark datasets for nonstationary learning. For instance, on a recent large-scale benchmark for nonstationary learning (~39M photos over a 10 year period), we show up to 15% relative accuracy gains through learned reweighting of training data.

The challenge of concept drift for supervised learning

To gain quantitative insight into slow concept drift, we built classifiers on a recent photo categorization task, comprising roughly 39M photographs sourced from social media websites over a 10 year period. We compared offline training, which iterated over all the training data multiple times in random order, and continual training, which iterated multiple times over each month of data in sequential (temporal) order. We measured model accuracy both during the training period and during a subsequent period where both models were frozen, i.e., not updated further on new data (shown below). At the end of the training period (left panel, x-axis = 0), both approaches have seen the same amount of data, but show a large performance gap. This is due to catastrophic forgetting, a problem in continual learning where a model’s knowledge of data from early on in the training sequence is diminished in an uncontrolled manner. On the other hand, forgetting has its advantages — over the test period (shown on the right), the continual trained model degrades much less rapidly than the offline model because it is less dependent on older data. The decay of both models’ accuracy in the test period is confirmation that the data is indeed evolving over time, and both models become increasingly less relevant.

Comparing offline and continually trained models on the photo classification task.

Time-sensitive reweighting of training data

We design a method combining the benefits of offline learning (the flexibility of effectively reusing all available data) and continual learning (the ability to downplay older data) to address slow concept drift. We build upon offline learning, then add careful control over the influence of past data and an optimization objective, both designed to reduce model decay in the future.

Suppose we wish to train a model, M, given some training data collected over time. We propose to also train a helper model that assigns a weight to each point based on its contents and age. This weight scales the contribution from that data point in the training objective for M. The objective of the weights is to improve the performance of M on future data.

In our work, we describe how the helper model can be meta-learned, i.e., learned alongside M in a manner that helps the learning of the model M itself. A key design choice of the helper model is that we separated out instance- and age-related contributions in a factored manner. Specifically, we set the weight by combining contributions from multiple different fixed timescales of decay, and learn an approximate “assignment” of a given instance to its most suited timescales. We find in our experiments that this form of the helper model outperforms many other alternatives we considered, ranging from unconstrained joint functions to a single timescale of decay (exponential or linear), due to its combination of simplicity and expressivity. Full details may be found in the paper.

Instance weight scoring

The top figure below shows that our learned helper model indeed up-weights more modern-looking objects in the CLEAR object recognition challenge; older-looking objects are correspondingly down-weighted. On closer examination (bottom figure below, gradient-based feature importance assessment), we see that the helper model focuses on the primary object within the image, as opposed to, e.g., background features that may spuriously be correlated with instance age.

Sample images from the CLEAR benchmark (camera & computer categories) assigned the highest and lowest weights respectively by our helper model.

Feature importance analysis of our helper model on sample images from the CLEAR benchmark.

Results

Gains on large-scale data

We first study the large-scale photo categorization task (PCAT) on the YFCC100M dataset discussed earlier, using the first five years of data for training and the next five years as test data. Our method (shown in red below) improves substantially over the no-reweighting baseline (black) as well as many other robust learning techniques. Interestingly, our method deliberately trades off accuracy on the distant past (training data unlikely to reoccur in the future) in exchange for marked improvements in the test period. Also, as desired, our method degrades less than other baselines in the test period.

Comparison of our method and relevant baselines on the PCAT dataset.

Broad applicability

We validated our findings on a wide range of nonstationary learning challenge datasets sourced from the academic literature (see 1, 2, 3, 4 for details) that spans data sources and modalities (photos, satellite images, social media text, medical records, sensor readings, tabular data) and sizes (ranging from 10k to 39M instances). We report significant gains in the test period when compared to the nearest published benchmark method for each dataset (shown below). Note that the previous best-known method may be different for each dataset. These results showcase the broad applicability of our approach.

Performance gain of our method on a variety of tasks studying natural concept drift. Our reported gains are over the previous best-known method for each dataset.

Extensions to continual learning

Finally, we consider an interesting extension of our work. The work above described how offline learning can be extended to handle concept drift using ideas inspired by continual learning. However, sometimes offline learning is infeasible — for example, if the amount of training data available is too large to maintain or process. We adapted our approach to continual learning in a straightforward manner by applying temporal reweighting within the context of each bucket of data being used to sequentially update the model. This proposal still retains some limitations of continual learning, e.g., model updates are performed only on most-recent data, and all optimization decisions (including our reweighting) are only made over that data. Nevertheless, our approach consistently beats regular continual learning as well as a wide range of other continual learning algorithms on the photo categorization benchmark (see below). Since our approach is complementary to the ideas in many baselines compared here, we anticipate even larger gains when combined with them.

Results of our method adapted to continual learning, compared to the latest baselines.

Conclusion

We addressed the challenge of data drift in learning by combining the strengths of previous approaches — offline learning with its effective reuse of data, and continual learning with its emphasis on more recent data. We hope that our work helps improve model robustness to concept drift in practice, and generates increased interest and new ideas in addressing the ubiquitous problem of slow concept drift.

Acknowledgements

We thank Mike Mozer for many interesting discussions in the early phase of this work, as well as very helpful advice and feedback during its development.

Source: Google AI Blog

Intervening on early readouts for mitigating spurious features and simplicity bias

Posted by Rishabh Tiwari, Pre-doctoral Researcher, and Pradeep Shenoy, Research Scientist, Google Research

Machine learning models in the real world are often trained on limited data that may contain unintended statistical biases. For example, in the CELEBA celebrity image dataset, a disproportionate number of female celebrities have blond hair, leading to classifiers incorrectly predicting “blond” as the hair color for most female faces — here, gender is a spurious feature for predicting hair color. Such unfair biases could have significant consequences in critical applications such as medical diagnosis.

Surprisingly, recent work has also discovered an inherent tendency of deep networks to amplify such statistical biases, through the so-called simplicity bias of deep learning. This bias is the tendency of deep networks to identify weakly predictive features early in the training, and continue to anchor on these features, failing to identify more complex and potentially more accurate features.

With the above in mind, we propose simple and effective fixes to this dual challenge of spurious features and simplicity bias by applying early readouts and feature forgetting. First, in “Using Early Readouts to Mediate Featural Bias in Distillation”, we show that making predictions from early layers of a deep network (referred to as “early readouts”) can automatically signal issues with the quality of the learned representations. In particular, these predictions are more often wrong, and more confidently wrong, when the network is relying on spurious features. We use this erroneous confidence to improve outcomes in model distillation, a setting where a larger “teacher” model guides the training of a smaller “student” model. Then in “Overcoming Simplicity Bias in Deep Networks using a Feature Sieve”, we intervene directly on these indicator signals by making the network “forget” the problematic features and consequently look for better, more predictive features. This substantially improves the model’s ability to generalize to unseen domains compared to previous approaches. Our AI Principles and our Responsible AI practices guide how we research and develop these advanced applications and help us address the challenges posed by statistical biases.

Animation comparing hypothetical responses from two models trained with and without the feature sieve.

Early readouts for debiasing distillation

We first illustrate the diagnostic value of early readouts and their application in debiased distillation, i.e., making sure that the student model inherits the teacher model’s resilience to feature bias through distillation. We start with a standard distillation framework where the student is trained with a mixture of label matching (minimizing the cross-entropy loss between student outputs and the ground-truth labels) and teacher matching (minimizing the KL divergence loss between student and teacher outputs for any given input).

Suppose one trains a linear decoder, i.e., a small auxiliary neural network named as Aux, on top of an intermediate representation of the student model. We refer to the output of this linear decoder as an early readout of the network representation. Our finding is that early readouts make more errors on instances that contain spurious features, and further, the confidence on those errors is higher than the confidence associated with other errors. This suggests that confidence on errors from early readouts is a fairly strong, automated indicator of the model’s dependence on potentially spurious features.

Illustrating the usage of early readouts (i.e., output from the auxiliary layer) in debiasing distillation. Instances that are confidently mispredicted in the early readouts are upweighted in the distillation loss.

We used this signal to modulate the contribution of the teacher in the distillation loss on a per-instance basis, and found significant improvements in the trained student model as a result.

We evaluated our approach on standard benchmark datasets known to contain spurious correlations (Waterbirds, CelebA, CivilComments, MNLI). Each of these datasets contain groupings of data that share an attribute potentially correlated with the label in a spurious manner. As an example, the CelebA dataset mentioned above includes groups such as {blond male, blond female, non-blond male, non-blond female}, with models typically performing the worst on the {non-blond female} group when predicting hair color. Thus, a measure of model performance is its worst group accuracy, i.e., the lowest accuracy among all known groups present in the dataset. We improved the worst group accuracy of student models on all datasets; moreover, we also improved overall accuracy in three of the four datasets, showing that our improvement on any one group does not come at the expense of accuracy on other groups. More details are available in our paper.

Comparison of Worst Group Accuracies of different distillation techniques relative to that of the Teacher model. Our method outperforms other methods on all datasets.

Overcoming simplicity bias with a feature sieve

In a second, closely related project, we intervene directly on the information provided by early readouts, to improve feature learning and generalization. The workflow alternates between identifying problematic features and erasing identified features from the network. Our primary hypothesis is that early features are more prone to simplicity bias, and that by erasing (“sieving”) these features, we allow richer feature representations to be learned.

Training workflow with feature sieve. We alternate between identifying problematic features (using training iteration) and erasing them from the network (using forgetting iteration).

We describe the identification and erasure steps in more detail:

Identifying simple features: We train the primary model and the readout model (AUX above) in conventional fashion via forward- and back-propagation. Note that feedback from the auxiliary layer does not back-propagate to the main network. This is to force the auxiliary layer to learn from already-available features rather than create or reinforce them in the main network.
Applying the feature sieve: We aim to erase the identified features in the early layers of the neural network with the use of a novel forgetting loss, L_f, which is simply the cross-entropy between the readout and a uniform distribution over labels. Essentially, all information that leads to nontrivial readouts are erased from the primary network. In this step, the auxiliary network and upper layers of the main network are kept unchanged.

We can control specifically how the feature sieve is applied to a given dataset through a small number of configuration parameters. By changing the position and complexity of the auxiliary network, we control the complexity of the identified- and erased features. By modifying the mixing of learning and forgetting steps, we control the degree to which the model is challenged to learn more complex features. These choices, which are dataset-dependent, are made via hyperparameter search to maximize validation accuracy, a standard measure of generalization. Since we include “no-forgetting” (i.e., the baseline model) in the search space, we expect to find settings that are at least as good as the baseline.

Below we show features learned by the baseline model (middle row) and our model (bottom row) on two benchmark datasets — biased activity recognition (BAR) and animal categorization (NICO). Feature importance was estimated using post-hoc gradient-based importance scoring (GRAD-CAM), with the orange-red end of the spectrum indicating high importance, while green-blue indicates low importance. Shown below, our trained models focus on the primary object of interest, whereas the baseline model tends to focus on background features that are simpler and spuriously correlated with the label.

Feature importance scoring using GRAD-CAM on activity recognition (BAR) and animal categorization (NICO) generalization benchmarks. Our approach (last row) focuses on the relevant objects in the image, whereas the baseline (ERM; middle row) relies on background features that are spuriously correlated with the label.

Through this ability to learn better, generalizable features, we show substantial gains over a range of relevant baselines on real-world spurious feature benchmark datasets: BAR, CelebA Hair, NICO and ImagenetA, by margins up to 11% (see figure below). More details are available in our paper.

Our feature sieve method improves accuracy by significant margins relative to the nearest baseline for a range of feature generalization benchmark datasets.

Conclusion

We hope that our work on early readouts and their use in feature sieving for generalization will both spur the development of a new class of adversarial feature learning approaches and help improve the generalization capability and robustness of deep learning systems.

Acknowledgements

The work on applying early readouts to debiasing distillation was conducted in collaboration with our academic partners Durga Sivasubramanian, Anmol Reddy and Prof. Ganesh Ramakrishnan at IIT Bombay. We extend our sincere gratitude to Praneeth Netrapalli and Anshul Nasery for their feedback and recommendations. We are also grateful to Nishant Jain, Shreyas Havaldar, Rachit Bansal, Kartikeya Badola, Amandeep Kaur and the whole cohort of pre-doctoral researchers at Google Research India for taking part in research discussions. Special thanks to Tom Small for creating the animation used in this post.

Source: Google AI Blog

Mixed-input matrix multiplication performance optimizations

Posted by Manish Gupta, Staff Software Engineer, Google Research

AI-driven technologies are weaving themselves into the fabric of our daily routines, with the potential to enhance our access to knowledge and boost our overall productivity. The backbone of these applications lies in large language models (LLMs). LLMs are memory-intensive and typically require specialized hardware accelerators to efficiently deliver tens of exaflops of computing power. This blog post shows how we can start addressing the computational challenges by utilizing memory more effectively.

The bulk of an LLM’s memory and compute are consumed by weights in matrix multiplication operations. Using narrower data types reduces memory consumption. For example, storing weights in the 8-bit integer (i.e., U8 or S8) data type reduces the memory footprint by 4× relative to single-precision (F32) and 2× relative to half-precision (F16) or bfloat16 (BF16). Furthermore, previous work has shown that LLM models running matrix multiplications with weights in S8 and input in F16 (preserving higher precision of the user-input) is an effective method for increasing the efficiency with acceptable trade-offs in accuracy. This technique is known as weight-only quantization and requires efficient implementation of matrix multiplication with mixed-inputs, e.g., half-precision input multiplied with 8-bits integer. Hardware accelerators, including GPUs, support a fixed set of data types, and thus, mixed-input matrix multiplication requires software transformations to map to the hardware operations.

To that end, in this blog we focus on mapping mixed-input matrix multiplication onto the NVIDIA Ampere architecture. We present software techniques addressing data type conversion and layout conformance to map mixed-input matrix multiplication efficiently onto hardware-supported data types and layouts. Our results show that the overhead of additional work in software is minimal and enables performance close to the peak hardware capabilities. The software techniques described here are released in the open-source NVIDIA/CUTLASS repository.

Memory footprint for an 175B parameter LLM model with various data types formats.

The matrix-multiply-accumulate operation

Modern AI hardware accelerators such as Google’s TPU and NVIDIA’s GPU multiply matrices natively in the hardware by targeting Tensor Cores, which are specialized processing elements to accelerate matrix operations, particularly for AI workloads. In this blog, we focus on NVIDIA Ampere Tensor Cores, which provide the matrix-multiply-accumulate (mma) operation. For the rest of the blog the reference to mma is for Ampere Tensor Cores. The supported data types, shapes, and data layout of the two input matrices (called operands) for the mma operation are fixed in hardware. This means that matrix multiplications with various data types and larger shapes are implemented in the software by tiling the problem onto hardware-supported data types, shapes, and layouts.

The Tensor Core mma operation is defined by specifying two input matrices (e.g., A & B, shown below) to produce a result matrix, C. The mma operation natively supports mixed-precision. Mixed-precision Tensor Cores allow mixing input (A and B) data type with the result (C) data type. In contrast, mixed-input matrix multiplication involves mixing the input data types, and it is not supported by the hardware, so it needs to be implemented in the software.

Tensor Core operation of M-by-N-by-K on input matrix A of M-by-K and matrix B of K-by-N produces output matrix C of M-by-N.

Challenges of mixed-input matrix multiplication

To simplify the discussion, we restrict to a specific example of mixed-input matrix multiplication: F16 for user input and U8 for the model weights (written as F16 * U8). The techniques described here work for various combinations of mixed-input data types.

A GPU programmer can access a hierarchy of memory, including global memory, shared memory, and registers, which are arranged in order of decreasing capacity but increasing speed. NVIDIA Ampere Tensor Core mma operations consume input matrices from registers. Furthermore, input and output matrices are required to conform to a layout of data within a group of 32 threads known as a warp. The supported data type and layout within a warp are fixed for an mma operation, so to implement mixed-input multiplication efficiently, it is necessary to solve the challenges of data type conversion and layout conformance in software.

Data type conversion

The mma operation requires two input matrices with the same data type. Thus, mixed-input matrix multiplication, where one of the operands is stored in U8 in global memory and other in F16, requires a data type conversion from U8 to F16. The conversion will bring two operands to F16, mapping the mixed-input matrix multiplication to hardware-supported mixed-precision Tensor Cores. Given the large number of weights, there are a large number of such operations, and our techniques show how to reduce their latency and improve performance.

Layout conformance

The mma operation also requires the layout of two input matrices, within the registers of a warp, to be conformat with hardware specification. The layout for the input matrix B of U8 data type in mixed-input matrix multiplication (F16 * U8) needs to conform with the converted F16 data type. This is called layout conformance and needs to be achieved in the software.

The figure below shows an mma operation consuming matrix A and matrix B from registers to produce matrix C in registers, distributed across one warp. The thread T0 is highlighted and zoomed in to show the weight matrix B goes through data type conversion and needs a layout conformance to be able to map to the hardware-supported Tensor Core operation.

The mapping of mixed-input (F32 = F16 * U8) operation in software to natively supported warp-level Tensor Cores in hardware (F32 = F16 * F16). (Original figure source Developing CUDA kernels to push Tensor Cores to the Absolute Limit on NVIDIA A100.)

Software strategies addressing challenges

A typical data type conversion involves a sequence of operations on 32-bit registers, shown below. Each rectangular block represents a register and the adjoining text are the operations. The entire sequence shows the conversion from 4xU8 to 2x(2xF16). The sequence involves roughly 10 operations.

NumericArrayConvertor from 4xU8 to 2x(2xF16) in 32-bit registers.

There are many ways of achieving layout conformance. Two of the existing solutions are:

Narrower bitwidth shared memory loads: In this approach, threads issue narrow bitwidth memory loads moving the U8 data from shared memory to registers. This results in two 32-bit registers, with each register containing 2xF16 values (shown above for the matrix B’s thread T0). The narrower shared memory load achieves layout conformance directly into registers without needing any shuffles; however, it does not utilize the full shared memory bandwidth.
Pre-processing in global memory: An alternative strategy involves rearranging the data within the global memory (one level above the shared memory in memory hierarchy), allowing wider shared memory loads. This approach maximizes the shared memory bandwidth utilization and ensures that the data is loaded in a conformant layout directly in the registers. Although the rearrangement process can be executed offline prior to the LLM deployment, ensuring no impact on the application performance, it introduces an additional, non-trivial hardware-specific pre-processing step that requires an extra program to rearrange the data. NVIDIA/FasterTransformer adopts this method to effectively address layout conformance challenges.

Optimized software strategies

To further optimize and reduce the overhead of data type conversion and layout conformance, we have implemented FastNumericArrayConvertor and FragmentShuffler, respectively.

FastNumericArrayConvertor operates on 4xU8 in 32-bit registers without unpacking individual 1xU8 values. Furthermore, it uses less expensive arithmetic operations which reduces the number of instructions and increases the speed of the conversion.

The conversion sequence for U8-to-F16 is shown below. The operations use packed 32b registers, avoiding explicit unpacking and packing. FastNumericArrayConvertor uses the permute byte to rearrange bytes of 4xU8 into two registers. Additionally, FastNumericArrayConvertor does not use expensive integer to floating-point conversion instructions and employs vectorized operations to obtain the packed results in two 32-bit registers containing 2x(2xF16) values. The FastNumericArrayConvertor for U8-to-F16 approximately uses six operations, a 1.6× reduction relative to the approach shown above.

FastNumericArrayConvertor utilizes permute bytes and packed arithmetic, reducing the number of instructions in the data type conversion.

FragmentShuffler handles the layout conformance by shuffling data in a way that allows the use of wider bitwidth load operation, increasing shared memory bandwidth utilization and reducing the total number of operations.

NVIDIA Ampere architecture provides a load matrix instruction (ldmatrix). The ldmatrix is a warp-level operation, where 32 threads of a warp move the data from shared memory to registers in the shape and layout that mma matrix A and B consume. The use of ldmatrix reduces the number of load instructions and increases the memory bandwidth utilization. Since the ldmatrix instruction moves U8 data to registers, the layout after the load conforms with U8*U8 mma operation, and not with F16*F16 mma operation. We implemented FragmentShuffler to rearrange the data within registers using shuffle (shfl.sync) operations to achieve the layout conformance.

The most significant contribution of this work is to achieve layout conformance through register shuffles, avoiding offline pre-processing in global memory or narrower bitwidth shared memory loads. Furthermore, we provide implementations for FastNumericArrayConvertor covering data type conversion from U8-to-F16, S8-to-F16, U8-to-BF16, and S8-to-BF16.

Performance results

We measured the performance of eight mixed-input variants of our method (shown below in blue and red; varying the data types of matrix A and B) and two mixed-precision data types (shown in green) on an NVIDIA A100 SXM chip. The performance results are shown in FLOPS (higher is better). Notably, the first eight matrix-multipications require additional operations relative to the last two, because the mixed-precision variants directly target hardware-accelerated Tensor Core operations and do not need data type conversion and layout conformance. Even so, our approach demonstrates mixed-input matrix multiplication performance only slightly below or on par with mixed-precision.

Mixed-input matrix multiplication performance on NVIDIA A100 40GB SMX4 chip for a compute-bound matrix problem shape m=3456, n=4096, k=2048.

Acknowledgements

We would like to mention several folks who have contributed through technical brainstorming and improving the blog post including, Quentin Colombet, Jacques Pienaar, Allie Culp, Calin Cascaval, Ashish Gondimalla, Matt Walsh, Marek Kolodziej, and Aman Bhatia. We would like to thank our NVIDIA partners Rawn Henry, Pradeep Ramani, Vijay Thakkar, Haicheng Wu, Andrew Kerr, Matthew Nicely, and Vartika Singh.

Source: Google AI Blog

Exphormer: Scaling transformers for graph-structured data

Posted by Ameya Velingker, Research Scientist, Google Research, and Balaji Venkatachalam, Software Engineer, Google

Graphs, in which objects and their relations are represented as nodes (or vertices) and edges (or links) between pairs of nodes, are ubiquitous in computing and machine learning (ML). For example, social networks, road networks, and molecular structure and interactions are all domains in which underlying datasets have a natural graph structure. ML can be used to learn the properties of nodes, edges, or entire graphs.

A common approach to learning on graphs are graph neural networks (GNNs), which operate on graph data by applying an optimizable transformation on node, edge, and global attributes. The most typical class of GNNs operates via a message-passing framework, whereby each layer aggregates the representation of a node with those of its immediate neighbors.

Recently, graph transformer models have emerged as a popular alternative to message-passing GNNs. These models build on the success of Transformer architectures in natural language processing (NLP), adapting them to graph-structured data. The attention mechanism in graph transformers can be modeled by an interaction graph, in which edges represent pairs of nodes that attend to each other. Unlike message passing architectures, graph transformers have an interaction graph that is separate from the input graph. The typical interaction graph is a complete graph, which signifies a full attention mechanism that models direct interactions between all pairs of nodes. However, this creates quadratic computational and memory bottlenecks that limit the applicability of graph transformers to datasets on small graphs with at most a few thousand nodes. Making graph transformers scalable has been considered one of the most important research directions in the field (see the first open problem here).

A natural remedy is to use a sparse interaction graph with fewer edges. Many sparse and efficient transformers have been proposed to eliminate the quadratic bottleneck for sequences, however, they do not generally extend to graphs in a principled manner.

In “Exphormer: Sparse Transformers for Graphs”, presented at ICML 2023, we address the scalability challenge by introducing a sparse attention framework for transformers that is designed specifically for graph data. The Exphormer framework makes use of expander graphs, a powerful tool from spectral graph theory, and is able to achieve strong empirical results on a wide variety of datasets. Our implementation of Exphormer is now available on GitHub.

Expander graphs

A key idea at the heart of Exphormer is the use of expander graphs, which are sparse yet well-connected graphs that have some useful properties — 1) the matrix representation of the graphs have similar linear-algebraic properties as a complete graph, and 2) they exhibit rapid mixing of random walks, i.e., a small number of steps in a random walk from any starting node is enough to ensure convergence to a “stable” distribution on the nodes of the graph. Expanders have found applications to diverse areas, such as algorithms, pseudorandomness, complexity theory, and error-correcting codes.

A common class of expander graphs are d-regular expanders, in which there are d edges from every node (i.e., every node has degree d). The quality of an expander graph is measured by its spectral gap, an algebraic property of its adjacency matrix (a matrix representation of the graph in which rows and columns are indexed by nodes and entries indicate whether pairs of nodes are connected by an edge). Those that maximize the spectral gap are known as Ramanujan graphs — they achieve a gap of d - 2*√(d-1), which is essentially the best possible among d-regular graphs. A number of deterministic and randomized constructions of Ramanujan graphs have been proposed over the years for various values of d. We use a randomized expander construction of Friedman, which produces near-Ramanujan graphs.

Expander graphs are at the heart of Exphormer. A good expander is sparse yet exhibits rapid mixing of random walks, making its global connectivity suitable for an interaction graph in a graph transformer model.

Exphormer replaces the dense, fully-connected interaction graph of a standard Transformer with edges of a sparse d-regular expander graph. Intuitively, the spectral approximation and mixing properties of an expander graph allow distant nodes to communicate with each other after one stacks multiple attention layers in a graph transformer architecture, even though the nodes may not attend to each other directly. Furthermore, by ensuring that d is constant (independent of the size of the number of nodes), we obtain a linear number of edges in the resulting interaction graph.

Exphormer: Constructing a sparse interaction graph

Exphormer combines expander edges with the input graph and virtual nodes. More specifically, the sparse attention mechanism of Exphormer builds an interaction graph consisting of three types of edges:

Edges from the input graph (local attention)
Edges from a constant-degree expander graph (expander attention)
Edges from every node to a small set of virtual nodes (global attention)

Exphormer builds an interaction graph by combining three types of edges. The resulting graph has good connectivity properties and retains the inductive bias of the input dataset graph while still remaining sparse.

Each component serves a specific purpose: the edges from the input graph retain the inductive bias from the input graph structure (which typically gets lost in a fully-connected attention module). Meanwhile, expander edges allow good global connectivity and random walk mixing properties (which spectrally approximate the complete graph with far fewer edges). Finally, virtual nodes serve as global “memory sinks” that can directly communicate with every node. While this results in additional edges from each virtual node equal to the number of nodes in the input graph, the resulting graph is still sparse. The degree of the expander graph and the number of virtual nodes are hyperparameters to tune for improving the quality metrics.

Furthermore, since we use an expander graph of constant degree and a small constant number of virtual nodes for the global attention, the resulting sparse attention mechanism is linear in the size of the original input graph, i.e., it models a number of direct interactions on the order of the total number of nodes and edges.

We additionally show that Exphormer is as expressive as the dense transformer and obeys universal approximation properties. In particular, when the sparse attention graph of Exphormer is augmented with self loops (edges connecting a node to itself), it can universally approximate continuous functions [1, 2].

Relation to sparse Transformers for sequences

It is interesting to compare Exphormer to sparse attention methods for sequences. Perhaps the architecture most conceptually similar to our approach is BigBird, which builds an interaction graph by combining different components. BigBird also uses virtual nodes, but, unlike Exphormer, it uses window attention and random attention from an Erdős-Rényi random graph model for the remaining components.

Window attention in BigBird looks at the tokens surrounding a token in a sequence — the local neighborhood attention in Exphormer can be viewed as a generalization of window attention to graphs.

The Erdős-Rényi graph on n nodes, G(n, p), which connects every pair of nodes independently with probability p, also functions as an expander graph for suitably high p. However, a superlinear number of edges (Ω(n log n)) is needed to ensure that an Erdős-Rényi graph is connected, let alone a good expander. On the other hand, the expanders used in Exphormer have only a linear number of edges.

Experimental results

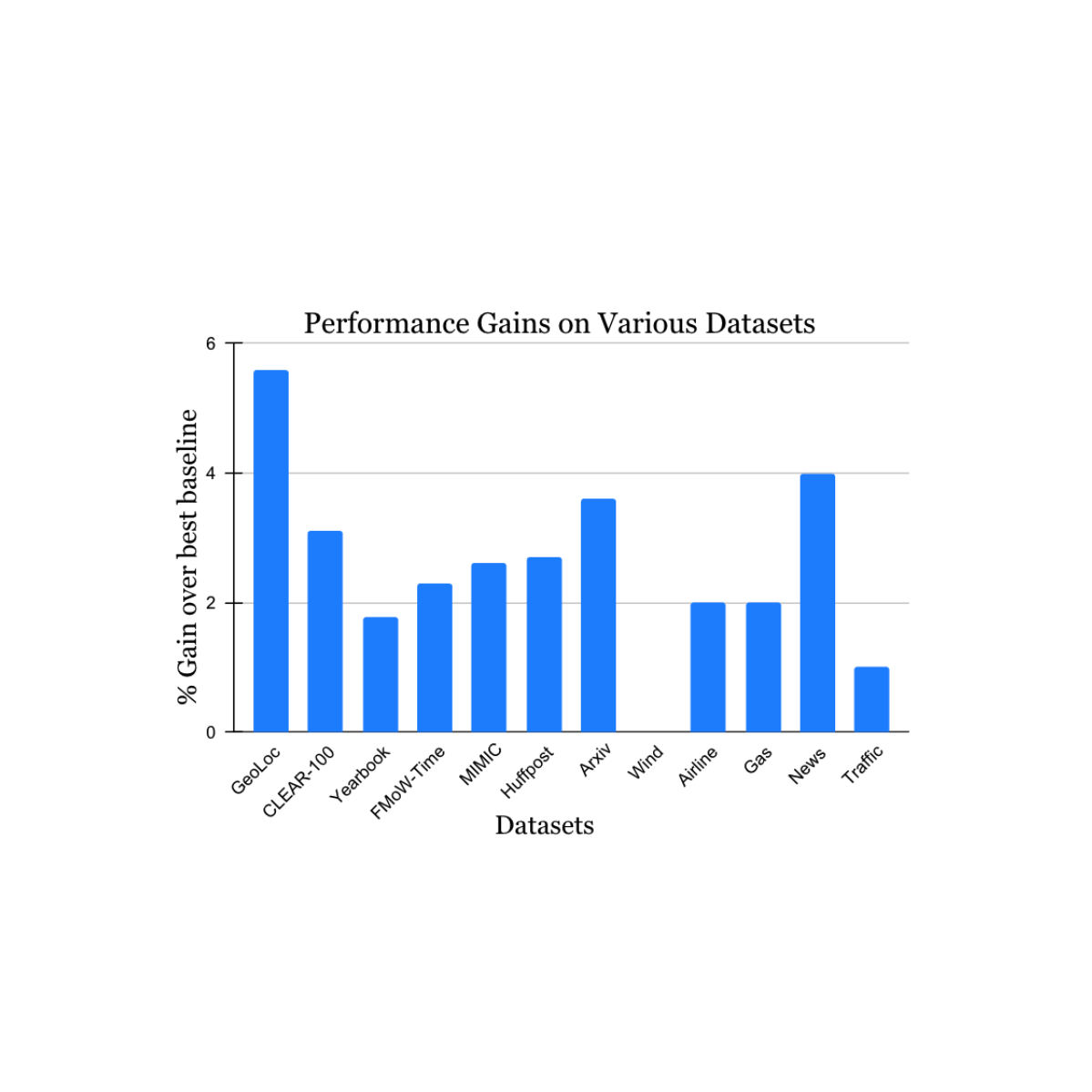
Earlier works have shown the use of full graph Transformer-based models on datasets with graphs of size up to 5,000 nodes. To evaluate the performance of Exphormer, we build upon the celebrated GraphGPS framework [3], which combines both message passing and graph transformers and achieves state-of-the-art performance on a number of datasets. We show that replacing dense attention with Exphormer for the graph attention component in the GraphGPS framework allows one to achieve models with comparable or better performance, often with fewer trainable parameters.

Furthermore, Exphormer notably allows graph transformer architectures to scale well beyond the usual graph size limits mentioned above. Exphormer can scale up to datasets of 10,000+ node graphs, such as the Coauthor dataset, and even beyond to larger graphs such as the well-known ogbn-arxiv dataset, a citation network, which consists of 170K nodes and 1.1 million edges.

Results comparing Exphormer to standard GraphGPS on the five Long Range Graph Benchmark datasets. We note that Exphormer achieved state-of-the-art results on four of the five datasets (PascalVOC-SP, COCO-SP, Peptides-Struct, PCQM-Contact) at the time of the paper’s publication.

Finally, we observe that Exphormer, which creates an overlay graph of small diameter via expanders, exhibits the ability to effectively learn long-range dependencies. The Long Range Graph Benchmark is a suite of five graph learning datasets designed to measure the ability of models to capture long-range interactions. Results show that Exphormer-based models outperform standard GraphGPS models (which were previously state-of-the-art on four out of five datasets at the time of publication).

Conclusion

Graph transformers have emerged as an important architecture for ML that adapts the highly successful sequence-based transformers used in NLP to graph-structured data. Scalability has, however, proven to be a major challenge in enabling the use of graph transformers on datasets with large graphs. In this post, we have presented Exphormer, a sparse attention framework that uses expander graphs to improve scalability of graph transformers. Exphormer is shown to have important theoretical properties and exhibit strong empirical performance, particularly on datasets where it is crucial to learn long range dependencies. For more information, we point the reader to a short presentation video from ICML 2023.

Acknowledgements

We thank our research collaborators Hamed Shirzad and Danica J. Sutherland from The University of British Columbia as well as Ali Kemal Sinop from Google Research. Special thanks to Tom Small for creating the animation used in this post.

Source: Google AI Blog

Sparsity-preserving differentially private training

Posted by Yangsibo Huang, Research Intern, Google Research; Chiyuan Zhang, Research Scientist, Google Research

Large embedding models have emerged as a fundamental tool for various applications in recommendation systems [1, 2] and natural language processing [3, 4, 5]. Such models enable the integration of non-numerical data into deep learning models by mapping categorical or string-valued input attributes with large vocabularies to fixed-length representation vectors using embedding layers. These models are widely deployed in personalized recommendation systems and achieve state-of-the-art performance in language tasks, such as language modeling, sentiment analysis, and question answering. In many such scenarios, privacy is an equally important feature when deploying those models. As a result, various techniques have been proposed to enable private data analysis. Among those, differential privacy (DP) is a widely adopted definition that limits exposure of individual user information while still allowing for the analysis of population-level patterns.

For training deep neural networks with DP guarantees, the most widely used algorithm is DP-SGD (DP stochastic gradient descent). One key component of DP-SGD is adding Gaussian noise to every coordinate of the gradient vectors during training. However, this creates scalability challenges when applied to large embedding models, because they rely on gradient sparsity for efficient training, but adding noise to all the coordinates destroys sparsity.

To mitigate this gradient sparsity problem, in “Sparsity-Preserving Differentially Private Training of Large Embedding Models” (to be presented at NeurIPS 2023), we propose a new algorithm called adaptive filtering-enabled sparse training (DP-AdaFEST). At a high level, the algorithm maintains the sparsity of the gradient by selecting only a subset of feature rows to which noise is added at each iteration. The key is to make such selections differentially private so that a three-way balance is achieved among the privacy cost, the training efficiency, and the model utility. Our empirical evaluation shows that DP-AdaFEST achieves a substantially sparser gradient, with a reduction in gradient size of over 10⁵X compared to the dense gradient produced by standard DP-SGD, while maintaining comparable levels of accuracy. This gradient size reduction could translate into 20X wall-clock time improvement.

Overview

To better understand the challenges and our solutions to the gradient sparsity problem, let us start with an overview of how DP-SGD works during training. As illustrated by the figure below, DP-SGD operates by clipping the gradient contribution from each example in the current random subset of samples (called a mini-batch), and adding coordinate-wise Gaussian noise to the average gradient during each iteration of stochastic gradient descent (SGD). DP-SGD has demonstrated its effectiveness in protecting user privacy while maintaining model utility in a variety of applications [6, 7].

An illustration of how DP-SGD works. During each training step, a mini-batch of examples is sampled, and used to compute the per-example gradients. Those gradients are processed through clipping, aggregation and summation of Gaussian noise to produce the final privatized gradients.

The challenges of applying DP-SGD to large embedding models mainly come from 1) the non-numerical feature fields like user/product IDs and categories, and 2) words and tokens that are transformed into dense vectors through an embedding layer. Due to the vocabulary sizes of those features, the process requires large embedding tables with a substantial number of parameters. In contrast to the number of parameters, the gradient updates are usually extremely sparse because each mini-batch of examples only activates a tiny fraction of embedding rows (the figure below visualizes the ratio of zero-valued coordinates, i.e., the sparsity, of the gradients under various batch sizes). This sparsity is heavily leveraged for industrial applications that efficiently handle the training of large-scale embeddings. For example, Google Cloud TPUs, custom-designed AI accelerators that are optimized for training and inference of large AI models, have dedicated APIs to handle large embeddings with sparse updates. This leads to significantly improved training throughput compared to training on GPUs, which at this time did not have specialized optimization for sparse embedding lookups. On the other hand, DP-SGD completely destroys the gradient sparsity because it requires adding independent Gaussian noise to all the coordinates. This creates a road block for private training of large embedding models as the training efficiency would be significantly reduced compared to non-private training.

Embedding gradient sparsity (the fraction of zero-value gradient coordinates) in the Criteo pCTR model (see below). The figure reports the gradient sparsity, averaged over 50 update steps, of the top five categorical features (out of a total of 26) with the highest number of buckets, as well as the sparsity of all categorical features. The sprasity decreases with the batch size as more examples hit more rows in the embedding table, creating non-zero gradients. However, the sparsity is above 0.97 even for very large batch sizes. This pattern is consistently observed for all the five features.

Algorithm

Our algorithm is built by extending standard DP-SGD with an extra mechanism at each iteration to privately select the “hot features”, which are the features that are activated by multiple training examples in the current mini-batch. As illustrated below, the mechanism works in a few steps:

Compute how many examples contributed to each feature bucket (we call each of the possible values of a categorical feature a “bucket”).
Restrict the total contribution from each example by clipping their counts.
Add Gaussian noise to the contribution count of each feature bucket.
Select only the features to be included in the gradient update that have a count above a given threshold (a sparsity-controlling parameter), thus maintaining sparsity. This mechanism is differentially private, and the privacy cost can be easily computed by composing it with the standard DP-SGD iterations.

Illustration of the process of the algorithm on a synthetic categorical feature that has 20 buckets. We compute the number of examples contributing to each bucket, adjust the value based on per-example total contributions (including those to other features), add Gaussian noise, and retain only those buckets with a noisy contribution exceeding the threshold for (noisy) gradient update.

Theoretical motivation

We provide the theoretical motivation that underlies DP-AdaFEST by viewing it as optimization using stochastic gradient oracles. Standard analysis of stochastic gradient descent in a theoretical setting decomposes the test error of the model into “bias” and “variance” terms. The advantage of DP-AdaFEST can be viewed as reducing variance at the cost of slightly increasing the bias. This is because DP-AdaFEST adds noise to a smaller set of coordinates compared to DP-SGD, which adds noise to all the coordinates. On the other hand, DP-AdaFEST introduces some bias to the gradients since the gradient on the embedding features are dropped with some probability. We refer the interested reader to Section 3.4 of the paper for more details.

Experiments

We evaluate the effectiveness of our algorithm with large embedding model applications, on public datasets, including one ad prediction dataset (Criteo-Kaggle) and one language understanding dataset (SST-2). We use DP-SGD with exponential selection as a baseline comparison.

The effectiveness of DP-AdaFEST is evident in the figure below, where it achieves significantly higher gradient size reduction (i.e., gradient sparsity) than the baseline while maintaining the same level of utility (i.e., only minimal performance degradation).

Specifically, on the Criteo-Kaggle dataset, DP-AdaFEST reduces the gradient computation cost of regular DP-SGD by more than 5x10⁵ times while maintaining a comparable AUC (which we define as a loss of less than 0.005). This reduction translates into a more efficient and cost-effective training process. In comparison, as shown by the green line below, the baseline method is not able to achieve reasonable cost reduction within such a small utility loss threshold.

In language tasks, there isn't as much potential for reducing the size of gradients, because the vocabulary used is often smaller and already quite compact (shown on the right below). However, the adoption of sparsity-preserving DP-SGD effectively obviates the dense gradient computation. Furthermore, in line with the bias-variance trade-off presented in the theoretical analysis, we note that DP-AdaFEST occasionally exhibits superior utility compared to DP-SGD when the reduction in gradient size is minimal. Conversely, when incorporating sparsity, the baseline algorithm faces challenges in maintaining utility.

A comparison of the best gradient size reduction (the ratio of the non-zero gradient value counts between regular DP-SGD and sparsity-preserving algorithms) achieved under ε =1.0 by DP-AdaFEST (our algorithm) and the baseline algorithm (DP-SGD with exponential selection) compared to DP-SGD at different thresholds for utility difference. A higher curve indicates a better utility/efficiency trade-off.

In practice, most ad prediction models are being continuously trained and evaluated. To simulate this online learning setup, we also evaluate with time-series data, which are notoriously challenging due to being non-stationary. Our evaluation uses the Criteo-1TB dataset, which comprises real-world user-click data collected over 24 days. Consistently, DP-AdaFEST reduces the gradient computation cost of regular DP-SGD by more than 10⁴ times while maintaining a comparable AUC.

A comparison of the best gradient size reduction achieved under ε =1.0 by DP-AdaFEST (our algorithm) and DP-SGD with exponential selection (a previous algorithm) compared to DP-SGD at different thresholds for utility difference. A higher curve indicates a better utility/efficiency trade-off. DP-AdaFEST consistently outperforms the previous method.

Conclusion

We present a new algorithm, DP-AdaFEST, for preserving gradient sparsity in differentially private training — particularly in applications involving large embedding models, a fundamental tool for various applications in recommendation systems and natural language processing. Our algorithm achieves significant reductions in gradient size while maintaining accuracy on real-world benchmark datasets. Moreover, it offers flexible options for balancing utility and efficiency via sparsity-controlling parameters, while our proposals offer much better privacy-utility loss.

Acknowledgements

This work was a collaboration with Badih Ghazi, Pritish Kamath, Ravi Kumar, Pasin Manurangsi and Amer Sinha.

Source: Google AI Blog

Alternating updates for efficient transformers

Posted by Xin Wang, Software Engineer, and Nishanth Dikkala, Research Scientist, Google Research

Contemporary deep learning models have been remarkably successful in many domains, ranging from natural language to computer vision. Transformer neural networks (transformers) are a popular deep learning architecture that today comprise the foundation for most tasks in natural language processing and also are starting to extend to applications in other domains, such as computer vision, robotics, and autonomous driving. Moreover, they form the backbone of all the current state-of-the-art language models.

Increasing scale in Transformer networks has led to improved performance and the emergence of behavior not present in smaller networks. However, this increase in scale often comes with prohibitive increases in compute cost and inference latency. A natural question is whether we can reap the benefits of larger models without incurring the computational burden.

In “Alternating Updates for Efficient Transformers”, accepted as a Spotlight at NeurIPS 2023, we introduce AltUp, a method to take advantage of increased token representation without increasing the computation cost. AltUp is easy to implement, widely applicable to any transformer architecture, and requires minimal hyperparameter tuning. For instance, using a variant of AltUp on a 770M parameter T5-Large model, the addition of ~100 parameters yields a model with a significantly better quality.

Background

To understand how we can achieve this, we dig into how transformers work. First, they partition the input into a sequence of tokens. Each token is then mapped to an embedding vector (via the means of an embedding table) called the token embedding. We call the dimension of this vector the token representation dimension. The Transformer then operates on this sequence of token embeddings by applying a series of computation modules (called layers) using its network parameters. The number of parameters in each transformer layer is a function of the layer’s width, which is determined by the token representation dimension.

To achieve benefits of scale without incurring the compute burden, prior works such as sparse mixture-of-experts (Sparse MoE) models (e.g., Switch Transformer, Expert Choice, V-MoE) have predominantly focused on efficiently scaling up the network parameters (in the self-attention and feedforward layers) by conditionally activating a subset based on the input. This allows us to scale up network size without significantly increasing compute per input. However, there is a research gap on scaling up the token representation dimension itself by conditionally activating parts of the token representation vector.

Recent works (for example, scaling laws and infinite-width networks) have empirically and theoretically established that a wider token representation helps in learning more complicated functions. This phenomenon is also evident in modern architectures of increasing capability. For instance, the representation dimension grows from 512 (small) to 768 (base) and 1024 (corresponding to models with 770M, 3B, and 11B parameters respectively) in T5 models, and from 4096 (8B) to 8192 (64B) and 18432 (540B) in PaLM models. A widened representation dimension also significantly improves performance for dual encoder retrieval models. However, naïvely widening the representation vector requires one to increase the model dimension accordingly, which quadratically¹ increases the amount of computation in the feedforward computation.

Method

AltUp works by partitioning a widened representation vector into equal sized blocks, processing only a single block at each layer, and using an efficient prediction-correction mechanism to infer the outputs of the other blocks (shown below on the right). This allows AltUp to simultaneously keep the model dimension, hence the computation cost, roughly constant and take advantage of using an increased token dimension. The increased token dimension allows the model to pack more information into each token’s embedding. By keeping the width of each transformer layer constant, AltUp avoids incurring the quadratic increase in computation cost that would otherwise be present with a naïve expansion of the representation.

An illustration of widening the token representation without (left) and with AltUp (right). This widening causes a near-quadratic increase in computation in a vanilla transformer due to the increased layer width. In contrast, Alternating Updates keeps the layer width constant and efficiently computes the output by operating on a sub-block of the representation at each layer.

More specifically, the input to each layer is two or more blocks, one of which is passed into the 1x width transformer layer (see figure below). We refer to this block as the “activated” block. This computation results in the exact output for the activated block. In parallel, we invoke a lightweight predictor that computes a weighted combination of all the input blocks. The predicted values, along with the computed value of the activated block, are passed on to a lightweight corrector that updates the predictions based on the observed values. This correction mechanism enables the inactivated blocks to be updated as a function of the activated one. Both the prediction and correction steps only involve a limited number of vector additions and multiplications and hence are much faster than a regular transformer layer. We note that this procedure can be generalized to an arbitrary number of blocks.

The predictor and corrector computations: The predictor mixes sub-blocks with trainable scalar coefficients; the corrector returns a weighted average of the predictor output and the transformer output. The predictor and corrector perform scalar-vector multiplications and incur negligible computation cost compared to the transformer. The predictor outputs a linear mixing of blocks with scalar mixing coefficients p_{i, j} , and the corrector combines predictor output and transformer output with weights g_i.

At a higher level, AltUp is similar to sparse MoE in that it is a method to add capacity to a model in the form of conditionally accessed (external) parameters. In sparse MoE, the additional parameters take the form of feed forward network (FFN) experts and the conditionality is with respect to the input. In AltUp, the external parameters come from the widened embedding table and the conditionality takes the form of alternating block-wise activation of the representation vector, as in the figure above. Hence, AltUp has the same underpinning as sparse MoE models.

An advantage of AltUp over sparse MoE is that it does not necessitate sharding since the number of additional parameters introduced is a factor² of the embedding table size, which typically makes up a small fraction of the overall model size. Moreover, since AltUp focuses on conditionally activating parts of a wider token representation, it can be applied synergistically with orthogonal techniques like MoE to obtain complementary performance gains.

Evaluation

AltUp was evaluated on T5 models on various benchmark language tasks. Models augmented with AltUp are uniformly faster than the extrapolated dense models at the same accuracy. For example, we observe that a T5 Large model augmented with AltUp leads to a 27%, 39%, 87%, and 29% speedup on GLUE, SuperGLUE, SQuAD, and Trivia-QA benchmarks, respectively.

Evaluations of AltUp on T5 models of various sizes and popular benchmarks. AltUp consistently leads to sizable speedups relative to baselines at the same accuracy. Latency is measured on TPUv3 with 8 cores. Speedup is defined as the change in latency divided by the AltUp latency (B = T5 Base, L = T5 Large, XL = T5 XL models).

AltUp’s relative performance improves as we apply it to larger models — compare the relative speedup of T5 Base + AltUp to that of T5 Large + AltUp. This demonstrates the scalability of AltUp and its improved performance on even larger models. Overall, AltUp consistently leads to models with better predictive performance than the corresponding baseline models with the same speed on all evaluated model sizes and benchmarks.

Extensions: Recycled AltUp

The AltUp formulation adds an insignificant amount of per-layer computation, however, it does require using a wider embedding table. In certain scenarios where the vocabulary size (i.e., the number of distinct tokens the tokenizer can produce) is very large, this may lead to a non-trivial amount of added computation for the initial embedding lookup and the final linear + softmax operation. A very large vocabulary may also lead to an undesirable amount of added embedding parameters. To address this, Recycled-AltUp is an extension of AltUp that avoids these computational and parameter costs by keeping the embedding table's width the same.

Illustration of the Architecture for Recycled-AltUp with K = 2.

In Recycled-AltUp, instead of widening the initial token embeddings, we replicate the embeddings K times to form a wider token representation. Hence, Recycled-AltUp adds virtually no additional parameters relative to the baseline transformer, while benefiting from a wider token representation.

Recycled-AltUp on T5-B/L/XL compared to baselines. Recycled-AltUp leads to strict improvements in pre-training performance without incurring any perceptible slowdown.

We also evaluate the lightweight extension of AltUp, Recycled-AltUp, with K = 2 on T5 base, large, and XL models and compare its pre-trained accuracy and speed to those of baselines. Since Recycled-AltUp does not require an expansion in the embedding table dimension, the models augmented with it have virtually the same number of trainable parameters as the baseline models. We again observe consistent improvements compared to the dense baselines.

Why does AltUp work?

AltUp increases a model’s capacity by adding and efficiently leveraging auxiliary parameters to the embedding table, and maintaining the higher dimensional representation across the layers. We believe that a key ingredient in this computation lies in AltUp’s prediction mechanism that performs an ensemble of the different blocks. This weighted combination enables continuous message passing to the entire vector despite activating only sub-blocks of it in each layer. Recycled-AltUp, on the other hand, does not add any additional parameters to the token embeddings. However, it still confers the benefit of simulating computation in a higher dimensional representation space since a higher dimensional representation vector is maintained when moving from one transformer layer to another. We conjecture that this aids the training by augmenting the flow of information through the network. An interesting research direction is to explore whether the benefits of Recycled-AltUp can be explained entirely by more favorable training dynamics.

Acknowledgements

We thank our collaborators Cenk Baykal, Dylan Cutler, and Rina Panigrahy at Google Research, and Nikhil Ghosh at University of California, Berkeley (work done during research internship at Google).

¹This is because the feedforward layers of a Transformer are typically scaled quadratically with the model dimension. ^↩
²This factor depends on the user-specified expansion factor, but is typically 1, i.e., we double the embedding table dimension. ^↩

Source: Google AI Blog

Grammar checking at Google Search scale

Posted by Eric Malmi, Senior Research Scientist, and Jakub Adamek, Senior Software Engineer, Google, Bard Team

Many people with questions about grammar turn to Google Search for guidance. While existing features, such as “Did you mean”, already handle simple typo corrections, more complex grammatical error correction (GEC) is beyond their scope. What makes the development of new Google Search features challenging is that they must have high precision and recall while outputting results quickly.

The conventional approach to GEC is to treat it as a translation problem and use autoregressive Transformer models to decode the response token-by-token, conditioning on the previously generated tokens. However, although Transformer models have proven to be effective at GEC, they aren’t particularly efficient because the generation cannot be parallelized due to autoregressive decoding. Often, only a few modifications are needed to make the input text grammatically correct, so another possible solution is to treat GEC as a text editing problem. If we could run the autoregressive decoder only to generate the modifications, that would substantially decrease the latency of the GEC model.

To this end, in “EdiT5: Semi-Autoregressive Text-Editing with T5 Warm-Start”, published at Findings of EMNLP 2022, we describe a novel text-editing model that is based on the T5 Transformer encoder-decoder architecture. EdiT5 powers the new Google Search grammar check feature that allows you to check if a phrase or sentence is grammatically correct and provides corrections when needed. Grammar check shows up when the phrase "grammar check" is included in a search query, and if the underlying model is confident about the correction. Additionally, it shows up for some queries that don’t contain the “grammar check” phrase when Search understands that is the likely intent.

Model architecture

For low-latency applications at Google, Transformer models are typically run on TPUs. Due to their fast matrix multiplication units (MMUs), these devices are optimized for performing large matrix multiplications quickly, for example running a Transformer encoder on hundreds of tokens in only a few milliseconds. In contrast, Transformer decoding makes poor use of a TPU’s capabilities, because it forces it to process only one token at a time. This makes autoregressive decoding the most time-consuming part of a translation-based GEC model.

In the EdiT5 approach, we reduce the number of decoding steps by treating GEC as a text editing problem. The EdiT5 text-editing model is based on the T5 Transformer encoder-decoder architecture with a few crucial modifications. Given an input with grammatical errors, the EdiT5 model uses an encoder to determine which input tokens to keep or delete. The kept input tokens form a draft output, which is optionally reordered using a non-autoregressive pointer network. Finally, a decoder outputs the tokens that are missing from the draft, and uses a pointing mechanism to indicate where each new token should be placed to generate a grammatically correct output. The decoder is only run to produce tokens that were missing in the draft, and as a result, runs for much fewer steps than would be needed in the translation approach to GEC.

To further decrease the decoder latency, we reduce the decoder down to a single layer, and we compensate by increasing the size of the encoder. Overall, this decreases latency significantly because the extra work in the encoder is efficiently parallelized.

Given an input with grammatical errors (“Guess when was I borned”), the EdiT5 model uses an encoder to determine which input tokens to keep (K) or delete (D), a pointer network (pointer) to reorder kept tokens, and a decoder to insert any new tokens that are needed to generate a grammatically correct output.

We applied the EdiT5 model to the public BEA grammatical error correction benchmark, comparing different model sizes. The experimental results show that an EdiT5 large model with 391M parameters yields a higher F0.5 score, which measures the accuracy of the corrections, while delivering a 9x speedup compared to a T5 base model with 248M parameters. The mean latency of the EdiT5 model was merely 4.1 milliseconds.

Performance of the T5 and EdiT5 models of various sizes on the public BEA GEC benchmark plotted against mean latency. Compared to T5, EdiT5 offers a better latency-F0.5 trade-off. Note that the x axis is logarithmic.

Improved training data with large language models

Our earlier research, as well as the results above, show that model size plays a crucial role in generating accurate grammatical corrections. To combine the advantages of large language models (LLMs) and the low latency of EdiT5, we leverage a technique called hard distillation. First, we train a teacher LLM using similar datasets used for the Gboard grammar model. The teacher model is then used to generate training data for the student EdiT5 model.

Training sets for grammar models consist of ungrammatical source / grammatical target sentence pairs. Some of the training sets have noisy targets that contain grammatical errors, unnecessary paraphrasing, or unwanted artifacts. Therefore, we generate new pseudo-targets with the teacher model to get cleaner and more consistent training data. Then, we re-train the teacher model with the pseudo-targets using a technique called self-training. Finally, we found that when the source sentence contains many errors, the teacher sometimes corrects only part of the errors. Thus, we can further improve the quality of the pseudo-targets by feeding them to the teacher LLM for a second time, a technique called iterative refinement.

Steps for training a large teacher model for grammatical error correction (GEC). Self-training and iterative refinement remove unnecessary paraphrasing, artifacts, and grammatical errors appearing in the original targets.

Putting it all together

Using the improved GEC data, we train two EdiT5-based models: a grammatical error correction model, and a grammaticality classifier. When the grammar check feature is used, we run the query first through the correction model, and then we check if the output is indeed correct with the classifier model. Only then do we surface the correction to the user.

The reason to have a separate classifier model is to more easily trade off between precision and recall. Additionally, for ambiguous or nonsensical queries to the model where the best correction is unclear, the classifier reduces the risk of serving erroneous or confusing corrections.

Conclusion

We have developed an efficient grammar correction model based on the state-of-the-art EdiT5 model architecture. This model allows users to check for the grammaticality of their queries in Google Search by including the “grammar check” phrase in the query.

Acknowledgements

We gratefully acknowledge the key contributions of the other team members, including Akash R, Aliaksei Severyn, Harsh Shah, Jonathan Mallinson, Mithun Kumar S R, Samer Hassan, Sebastian Krause, and Shikhar Thakur. We’d also like to thank Felix Stahlberg, Shankar Kumar, and Simon Tong for helpful discussions and pointers.

Source: Google AI Blog

Batch calibration: Rethinking calibration for in-context learning and prompt engineering

Posted by Han Zhou, Student Researcher, and Subhrajit Roy, Senior Research Scientist, Google Research

Prompting large language models (LLMs) has become an efficient learning paradigm for adapting LLMs to a new task by conditioning on human-designed instructions. The remarkable in-context learning (ICL) ability of LLMs also leads to efficient few-shot learners that can generalize from few-shot input-label pairs. However, the predictions of LLMs are highly sensitive and even biased to the choice of templates, label spaces (such as yes/no, true/false, correct/incorrect), and demonstration examples, resulting in unexpected performance degradation and barriers for pursuing robust LLM applications. To address this problem, calibration methods have been developed to mitigate the effects of these biases while recovering LLM performance. Though multiple calibration solutions have been provided (e.g., contextual calibration and domain-context calibration), the field currently lacks a unified analysis that systematically distinguishes and explains the unique characteristics, merits, and downsides of each approach.

With this in mind, in “Batch Calibration: Rethinking Calibration for In-Context Learning and Prompt Engineering”, we conduct a systematic analysis of the existing calibration methods, where we both provide a unified view and reveal the failure cases. Inspired by these analyses, we propose Batch Calibration (BC), a simple yet intuitive method that mitigates the bias from a batch of inputs, unifies various prior approaches, and effectively addresses the limitations in previous methods. BC is zero-shot, self-adaptive (i.e., inference-only), and incurs negligible additional costs. We validate the effectiveness of BC with PaLM 2 and CLIP models and demonstrate state-of-the-art performance over previous calibration baselines across more than 10 natural language understanding and image classification tasks.

Motivation

In pursuit of practical guidelines for ICL calibration, we started with understanding the limitations of current methods. We find that the calibration problem can be framed as an unsupervised decision boundary learning problem. We observe that uncalibrated ICL can be biased towards predicting a class, which we explicitly refer to as contextual bias, the a priori propensity of LLMs to predict certain classes over others unfairly given the context. For example, the prediction of LLMs can be biased towards predicting the most frequent label, or the label towards the end of the demonstration. We find that, while theoretically more flexible, non-linear boundaries (prototypical calibration) tend to be susceptible to overfitting and may suffer from instability for challenging multi-class tasks. Conversely, we find that linear decision boundaries can be more robust and generalizable across tasks. In addition, we find that relying on additional content-free inputs (e.g., “N/A” or random in-domain tokens) as the grounds for estimating the contextual bias is not always optimal and may even introduce additional bias, depending on the task type.

Batch calibration

Inspired by the previous discussions, we designed BC to be a zero-shot, inference-only and generalizable calibration technique with negligible computation cost. We argue that the most critical component for calibration is to accurately estimate the contextual bias. We, therefore, opt for a linear decision boundary for its robustness, and instead of relying on content-free inputs, we propose to estimate the contextual bias for each class from a batch in a content-based manner by marginalizing the output score over all samples within the batch, which is equivalent to measuring the mean score for each class (visualized below).

We then obtain the calibrated probability by dividing the output probability over the contextual prior, which is equivalent to aligning the log-probability (LLM scores) distribution to the estimated mean of each class. It is noteworthy that because it requires no additional inputs to estimate the bias, this BC procedure is zero-shot, only involves unlabeled test samples, and incurs negligible computation costs. We may either compute the contextual bias once all test samples are seen, or alternatively, in an on-the-fly manner that dynamically processes the outputs. To do so, we may use a running estimate of the contextual bias for BC, thereby allowing BC's calibration term to be estimated from a small number of mini-batches that is subsequently stabilized when more mini-batches arrive.

Illustration of Batch Calibration (BC). Batches of demonstrations with in-context examples and test samples are passed into the LLM. Due to sources of implicit bias in the context, the score distribution from the LLM becomes biased. BC is a modular and adaptable layer option appended to the output of the LLM that generates calibrated scores (visualized for illustration only).

Experiment design

For natural language tasks, we conduct experiments on 13 more diverse and challenging classification tasks, including the standard GLUE and SuperGLUE datasets. This is in contrast to previous works that only report on relatively simple single-sentence classification tasks.. For image classification tasks, we include SVHN, EuroSAT, and CLEVR. We conduct experiments mainly on the state-of-the-art PaLM 2 with size variants PaLM 2-S, PaLM 2-M, and PaLM 2-L. For VLMs, we report the results on CLIP ViT-B/16.

Results

Notably, BC consistently outperforms ICL, yielding a significant performance enhancement of 8% and 6% on small and large variants of PaLM 2, respectively. This shows that the BC implementation successfully mitigates the contextual bias from the in-context examples and unleashes the full potential of LLM in efficient learning and quick adaptation to new tasks. In addition, BC improves over the state-of-the-art prototypical calibration (PC) baseline by 6% on PaLM 2-S, and surpasses the competitive contextual calibration (CC) baseline by another 3% on average on PaLM 2-L. Specifically, BC is a generalizable and cheaper technique across all evaluated tasks, delivering stable performance improvement, whereas previous baselines exhibit varying degrees of performance across tasks.

Batch Calibration (BC) achieves the best performance on 1-shot ICL over calibration baselines: contextual calibration (CC), domain-context calibration (DC), and prototypical calibration (PC) on an average of 13 NLP tasks on PaLM 2 and outperforms the zero-shot CLIP on image tasks.

We analyze the performance of BC by varying the number of ICL shots from 0 to 4, and BC again outperforms all baseline methods. We also observe an overall trend for improved performance when more shots are available, where BC demonstrates the best stability.

The ICL performance on various calibration techniques over the number of ICL shots on PaLM 2-S. We compare BC with the uncalibrated ICL, contextual calibration (CC), domain-context calibration (DC), and prototypical calibration (PC) baselines.

We further visualize the decision boundaries of uncalibrated ICL after applying existing calibration methods and the proposed BC. We show success and failure cases for each baseline method, whereas BC is consistently effective.

Visualization of the decision boundaries of uncalibrated ICL, and after applying existing calibration methods and the proposed BC in representative binary classification tasks of SST-2 (top row) and QNLI (bottom row) on 1-shot PaLM 2-S. Each axis indicates the LLM score on the defined label.

Robustness and ablation studies

We analyze the robustness of BC with respect to common prompt engineering design choices that were previously shown to significantly affect LLM performance: choices and orders of in-context examples, the prompt template for ICL, and the label space. First, we find that BC is more robust to ICL choices and can mostly achieve the same performance with different ICL examples. Additionally, given a single set of ICL shots, altering the order between each ICL example has minimal impact on the BC performance. Furthermore, we analyze the robustness of BC under 10 designs of prompt templates, where BC shows consistent improvement over the ICL baseline. Therefore, though BC improves performance, a well-designed template can further enhance the performance of BC. Lastly, we examine the robustness of BC to variations in label space designs (see appendix in our paper). Remarkably, even when employing unconventional choices such as emoji pairs as labels, leading to dramatic oscillations of ICL performance, BC largely recovers performance. This observation demonstrates that BC increases the robustness of LLM predictions under common prompt design choices and makes prompt engineering easier.

Batch Calibration makes prompt engineering easier while being data-efficient. Data are visualized as a standard box plot, which illustrates values for the median, first and third quartiles, and minimum and maximum.

Moreover, we study the impact of batch size on the performance of BC. In contrast to PC, which also leverages an unlabeled estimate set, BC is remarkably more sample efficient, achieving a strong performance with only around 10 unlabeled samples, whereas PC requires more than 500 unlabeled samples before its performance stabilizes.

Batch Calibration makes prompt engineering easier while being insensitive to the batch size.

Conclusion

We first revisit previous calibration methods while addressing two critical research questions from an interpretation of decision boundaries, revealing their failure cases and deficiencies. We then propose Batch Calibration, a zero-shot and inference-only calibration technique. While methodologically simple and easy to implement with negligible computation cost, we show that BC scales from a language-only setup to the vision-language context, achieving state-of-the-art performance in both modalities. BC significantly improves the robustness of LLMs with respect to prompt designs, and we expect easy prompt engineering with BC.

Acknowledgements

This work was conducted by Han Zhou, Xingchen Wan, Lev Proleev, Diana Mincu, Jilin Chen, Katherine Heller, Subhrajit Roy. We would like to thank Mohammad Havaei and other colleagues at Google Research for their discussion and feedback.