One of the primary challenges for the realization of near-term quantum computers has to do with their most basic constituent: the qubit. Qubits can interact with anything in close proximity that carries energy close to their own—stray photons (i.e., unwanted electromagnetic fields), phonons (mechanical oscillations of the quantum device), or quantum defects (irregularities in the substrate of the chip formed during manufacturing)—which can unpredictably change the state of the qubits themselves.
Further complicating matters, there are numerous challenges posed by the tools used to control qubits. Manipulating and reading out qubits is performed via classical controls: analog signals in the form of electromagnetic fields coupled to a physical substrate in which the qubit is embedded, e.g., superconducting circuits. Imperfections in these control electronics (giving rise to white noise), interference from external sources of radiation, and fluctuations in digital-to-analog converters, introduce even more stochastic errors that degrade the performance of quantum circuits. These practical issues impact the fidelity of the computation and thus limit the applications of near-term quantum devices.
To improve the computational capacity of quantum computers, and to pave the road towards large-scale quantum computation, it is necessary to first build physical models that accurately describe these experimental problems.
In “Universal Quantum Control through Deep Reinforcement Learning”, published in Nature Partner Journal (npj) Quantum Information, we present a new quantum control framework generated using deep reinforcement learning, where various practical concerns in quantum control optimization can be encapsulated by a single control cost function. Our framework provides a reduction in the average quantum logic gate error of up to two orders-of-magnitude over standard stochastic gradient descent solutions and a significant decrease in gate time from optimal gate synthesis counterparts. Our results open a venue for wider applications in quantum simulation, quantum chemistry and quantum supremacy tests using near-term quantum devices.
The novelty of this new quantum control paradigm hinges upon the development of a quantum control function and an efficient optimization method based on deep reinforcement learning. To develop a comprehensive cost function, we first need to develop a physical model for the realistic quantum control process, one where we are able to reliably predict the amount of error. One of the most detrimental errors to the accuracy of quantum computation is leakage: the amount of quantum information lost during the computation. Such information leakage usually occurs when the quantum state of a qubit gets excited to a higher energy state, or decays to a lower energy state through spontaneous emission. Leakage errors not only lose useful quantum information, they also degrade the “quantumness” and eventually reduce the performance of a quantum computer to that of a classical one.
A common practice to accurately evaluate the leaked information during the quantum computation is to simulate the whole computation first. However, this defeats the purpose of building large-scale quantum computers, since their advantage is that they are able to perform calculations infeasible for classical systems. With improved physical modeling, our generic cost function enables a joint optimization over the accumulated leakage errors, violations of control boundary conditions, total gate time, and gate fidelity.
With the new quantum control cost function in hand, the next step is to apply an efficient optimization tool to minimize it. Existing optimization methods turn out to be unsatisfactory in finding high fidelity solutions that are also robust to control fluctuations. Instead, we apply an on-policy deep reinforcement learning (RL) method, trusted-region RL, since this method exhibits good performance in all benchmark problems, is inherently robust to sample noise, and has the capability to optimize hard control problems with hundreds of millions of control parameters. The salient difference between this on-policy RL from previously studied off-policy RL methods is that the control policy is represented independently from the control cost. Off-policy RL, such as Q-learning, on the other hand, uses a single neural network (NN) to represent both the control trajectory, and the associated reward, where the control trajectory specifies the control signals to be coupled to qubits at different time steps, and the associated award evaluates how good the current step of the quantum control is.
On-policy RL is well known for its ability to leverage non-local features in control trajectories, which becomes crucial when the control landscape is high-dimensional and packed with a combinatorially large number of non-global solutions, as is often the case for quantum systems.
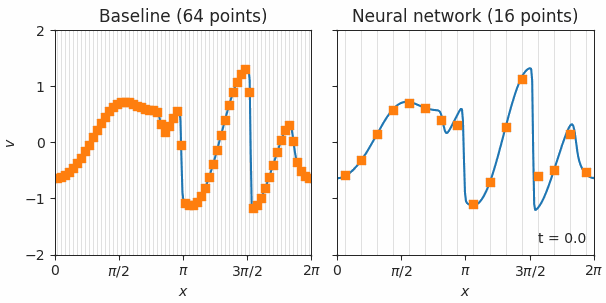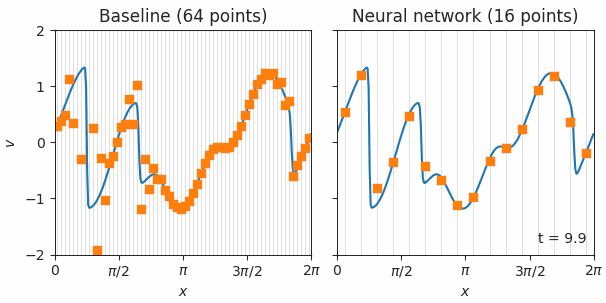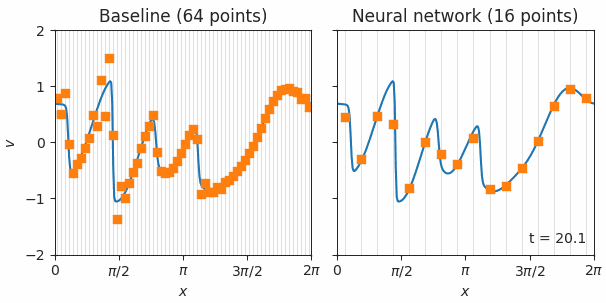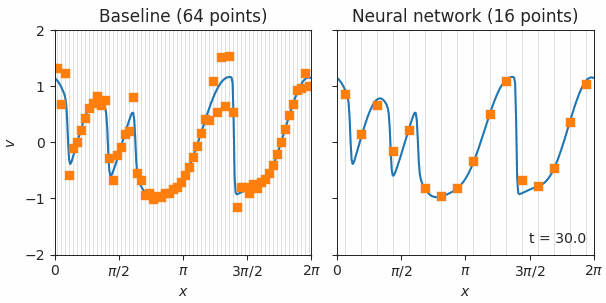
We encode the control trajectory into a three-layer, fully connected NN—the policy NN—and the control cost function into a second NN—the value NN—which encodes the discounted future reward. Robust control solutions were obtained by reinforcement learning agents, which trains both NNs under a stochastic environment that mimics a realistic noisy control actuation. We provide control solutions to a set of continuously parameterized two-qubit quantum gates that are important for quantum chemistry applications but are costly to implement using the conventional universal gate set.
Under this new framework, our numerical simulations show a 100x reduction in quantum gate errors and reduced gate times for a family of continuously parameterized simulation gates by an average of one order-of-magnitude over traditional approaches using a universal gate set.
This work highlights the importance of using novel machine learning techniques and near-term quantum algorithms that leverage the flexibility and additional computational capacity of a universal quantum control scheme. More experiments are needed to integrate machine learning techniques, such as the one developed in this work, into practical quantum computation procedures to fully improve its computational capacity through machine learning.