Tag Archives: Social Networks

STUDY: Socially aware temporally causal decoder recommender systems

Posted by Eltayeb Ahmed, Research Engineer, and Subhrajit Roy, Senior Research Scientist, Google Research

Reading has many benefits for young students, such as better linguistic and life skills, and reading for pleasure has been shown to correlate with academic success. Furthermore students have reported improved emotional wellbeing from reading, as well as better general knowledge and better understanding of other cultures. With the vast amount of reading material both online and off, finding age-appropriate, relevant and engaging content can be a challenging task, but helping students do so is a necessary step to engage them in reading. Effective recommendations that present students with relevant reading material helps keep students reading, and this is where machine learning (ML) can help.

ML has been widely used in building recommender systems for various types of digital content, ranging from videos to books to e-commerce items. Recommender systems are used across a range of digital platforms to help surface relevant and engaging content to users. In these systems, ML models are trained to suggest items to each user individually based on user preferences, user engagement, and the items under recommendation. These data provide a strong learning signal for models to be able to recommend items that are likely to be of interest, thereby improving user experience.

In “STUDY: Socially Aware Temporally Causal Decoder Recommender Systems”, we present a content recommender system for audiobooks in an educational setting taking into account the social nature of reading. We developed the STUDY algorithm in partnership with Learning Ally, an educational nonprofit, aimed at promoting reading in dyslexic students, that provides audiobooks to students through a school-wide subscription program. Leveraging the wide range of audiobooks in the Learning Ally library, our goal is to help students find the right content to help boost their reading experience and engagement. Motivated by the fact that what a person’s peers are currently reading has significant effects on what they would find interesting to read, we jointly process the reading engagement history of students who are in the same classroom. This allows our model to benefit from live information about what is currently trending within the student’s localized social group, in this case, their classroom.


Data

Learning Ally has a large digital library of curated audiobooks targeted at students, making it well-suited for building a social recommendation model to help improve student learning outcomes. We received two years of anonymized audiobook consumption data. All students, schools and groupings in the data were anonymized, only identified by a randomly generated ID not traceable back to real entities by Google. Furthermore all potentially identifiable metadata was only shared in an aggregated form, to protect students and institutions from being re-identified. The data consisted of time-stamped records of student’s interactions with audiobooks. For each interaction we have an anonymized student ID (which includes the student’s grade level and anonymized school ID), an audiobook identifier and a date. While many schools distribute students in a single grade across several classrooms, we leverage this metadata to make the simplifying assumption that all students in the same school and in the same grade level are in the same classroom. While this provides the foundation needed to build a better social recommender model, it's important to note that this does not enable us to re-identify individuals, class groups or schools.


The STUDY algorithm

We framed the recommendation problem as a click-through rate prediction problem, where we model the conditional probability of a user interacting with each specific item conditioned on both 1) user and item characteristics and 2) the item interaction history sequence for the user at hand. Previous work suggests Transformer-based models, a widely used model class developed by Google Research, are well suited for modeling this problem. When each user is processed individually this becomes an autoregressive sequence modeling problem. We use this conceptual framework to model our data and then extend this framework to create the STUDY approach.

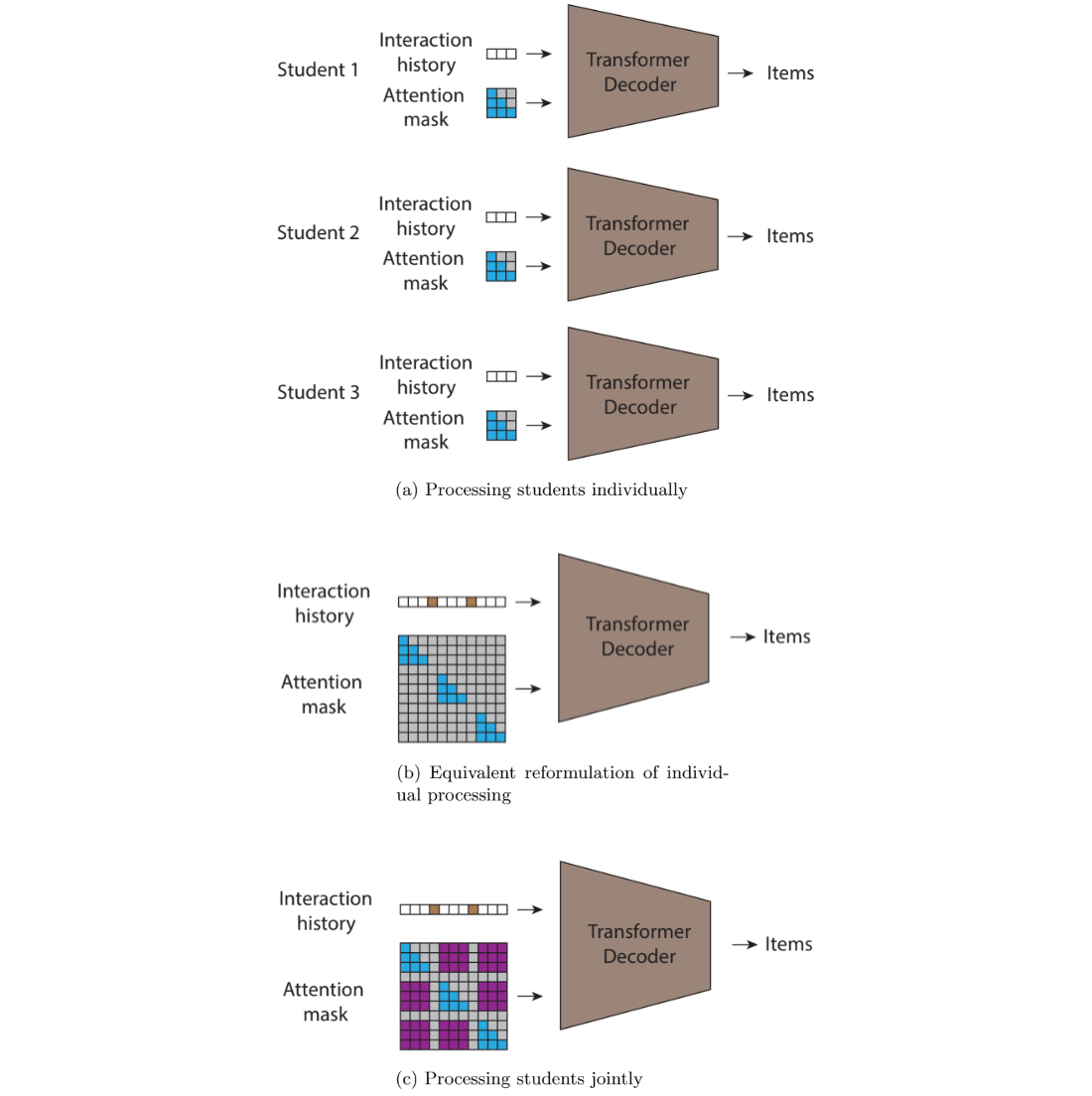
While this approach for click-through rate prediction can model dependencies between past and future item preferences for an individual user and can learn patterns of similarity across users at train time, it cannot model dependencies across different users at inference time. To recognise the social nature of reading and remediate this shortcoming we developed the STUDY model, which concatenates multiple sequences of books read by each student into a single sequence that collects data from multiple students in a single classroom.

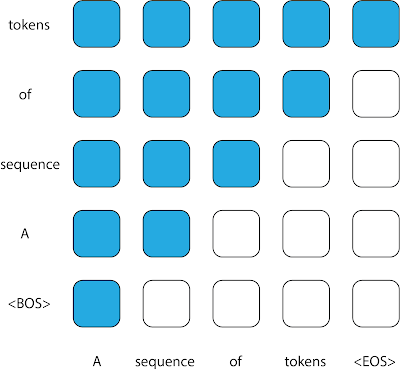
However, this data representation requires careful diligence if it is to be modeled by transformers. In transformers, the attention mask is the matrix that controls which inputs can be used to inform the predictions of which outputs. The pattern of using all prior tokens in a sequence to inform the prediction of an output leads to the upper triangular attention matrix traditionally found in causal decoders. However, since the sequence fed into the STUDY model is not temporally ordered, even though each of its constituent subsequences is, a standard causal decoder is no longer a good fit for this sequence. When trying to predict each token, the model is not allowed to attend to every token that precedes it in the sequence; some of these tokens might have timestamps that are later and contain information that would not be available at deployment time.

In this figure we show the attention mask typically used in causal decoders. Each column represents an output and each column represents an output. A value of 1 (shown as blue) for a matrix entry at a particular position denotes that the model can observe the input of that row when predicting the output of the corresponding column, whereas a value of 0 (shown as white) denotes the opposite.

The STUDY model builds on causal transformers by replacing the triangular matrix attention mask with a flexible attention mask with values based on timestamps to allow attention across different subsequences. Compared to a regular transformer, which would not allow attention across different subsequences and would have a triangular matrix mask within sequence, STUDY maintains a causal triangular attention matrix within a sequence and has flexible values across sequences with values that depend on timestamps. Hence, predictions at any output point in the sequence are informed by all input points that occurred in the past relative to the current time point, regardless of whether they appear before or after the current input in the sequence. This causal constraint is important because if it is not enforced at train time, the model could potentially learn to make predictions using information from the future, which would not be available for a real world deployment.

In (a) we show a sequential autoregressive transformer with causal attention that processes each user individually; in (b) we show an equivalent joint forward pass that results in the same computation as (a); and finally, in (c) we show that by introducing new nonzero values (shown in purple) to the attention mask we allow information to flow across users. We do this by allowing a prediction to condition on all interactions with an earlier timestamp, irrespective of whether the interaction came from the same user or not.

Experiments

We used the Learning Ally dataset to train the STUDY model along with multiple baselines for comparison. We implemented an autoregressive click-through rate transformer decoder, which we refer to as “Individual”, a k-nearest neighbor baseline (KNN), and a comparable social baseline, social attention memory network (SAMN). We used the data from the first school year for training and we used the data from the second school year for validation and testing.

We evaluated these models by measuring the percentage of the time the next item the user actually interacted with was in the model’s top n recommendations, i.e., hits@n, for different values of n. In addition to evaluating the models on the entire test set we also report the models’ scores on two subsets of the test set that are more challenging than the whole data set. We observed that students will typically interact with an audiobook over multiple sessions, so simply recommending the last book read by the user would be a strong trivial recommendation. Hence, the first test subset, which we refer to as “non-continuation”, is where we only look at each model’s performance on recommendations when the students interact with books that are different from the previous interaction. We also observe that students revisit books they have read in the past, so strong performance on the test set can be achieved by restricting the recommendations made for each student to only the books they have read in the past. Although there might be value in recommending old favorites to students, much value from recommender systems comes from surfacing content that is new and unknown to the user. To measure this we evaluate the models on the subset of the test set where the students interact with a title for the first time. We name this evaluation subset “novel”.

We find that STUDY outperforms all other tested models across almost every single slice we evaluated against.

In this figure we compare the performance of four models, Study, Individual, KNN and SAMN. We measure the performance with hits@5, i.e., how likely the model is to suggest the next title the user read within the model’s top 5 recommendations. We evaluate the model on the entire test set (all) as well as the novel and non-continuation splits. We see STUDY consistently outperforms the other three models presented across all splits.

Importance of appropriate grouping

At the heart of the STUDY algorithm is organizing users into groups and doing joint inference over multiple users who are in the same group in a single forward pass of the model. We conducted an ablation study where we looked at the importance of the actual groupings used on the performance of the model. In our presented model we group together all students who are in the same grade level and school. We then experiment with groups defined by all students in the same grade level and district and also place all students in a single group with a random subset used for each forward pass. We also compare these models against the Individual model for reference.

We found that using groups that were more localized was more effective, with the school and grade level grouping outperforming the district and grade level grouping. This supports the hypothesis that the STUDY model is successful because of the social nature of activities such as reading — people’s reading choices are likely to correlate with the reading choices of those around them. Both of these models outperformed the other two models (single group and Individual) where grade level is not used to group students. This suggests that data from users with similar reading levels and interests is beneficial for performance.


Future work

This work is limited to modeling recommendations for user populations where the social connections are assumed to be homogenous. In the future it would be beneficial to model a user population where relationships are not homogeneous, i.e., where categorically different types of relationships exist or where the relative strength or influence of different relationships is known.


Acknowledgements

This work involved collaborative efforts from a multidisciplinary team of researchers, software engineers and educational subject matter experts. We thank our co-authors: Diana Mincu, Lauren Harrell, and Katherine Heller from Google. We also thank our colleagues at Learning Ally, Jeff Ho, Akshat Shah, Erin Walker, and Tyler Bastian, and our collaborators at Google, Marc Repnyek, Aki Estrella, Fernando Diaz, Scott Sanner, Emily Salkey and Lev Proleev.

Source: Google AI Blog


Understanding the Shape of Large-Scale Data

Posted by Anton Tsitsulin, Research Intern and Bryan Perozzi, Senior Research Scientist, Graph Mining Team, Google Research

Understanding the differences and similarities between complex datasets is an interesting challenge that often arises when working with data. One way to formalize this question is to view each dataset as a graph, a mathematical model for how items relate to each other. Graphs are widely used to model relationships between objects — the Internet graph connects pages referencing each other, social graphs link together friends, and molecule graphs connect atoms bonding with each other.
Graphs are discrete objects that can model the relationships between many different types of data, including web pages (left), social connections (center), or molecules (right).
Once there is a collection of multiple graphs, it is common to want to predict some property of each one as an aggregate (i.e., one label per graph). For example, consider the task of predicting protein function from structure: each dataset here is one protein, and the prediction task is whether the final structure encodes an enzyme or not. Since one wants a model to actually compute the prediction, we need a representation that lets us generalize across different protein structures. Ideally, one would want a way to represent graphs as vectors without costly labelling. The problem becomes harder with increasing graph size — in the molecule case humans possess some knowledge about their properties, however, reasoning about larger, more complex datasets becomes increasingly difficult.

In this post we highlight some recent advances in the area of graph representation learning with “Just SLaQ When You Approximate: Accurate Spectral Distances for Web-Scale Graphs” (published at WWW'20), a publication that improves on the scalability of our earlier research, “DDGK: Learning Graph Representations for Deep Divergence Graph Kernels” (published at WWW’19). SLaQ introduces a way to scale computations to approximate a certain class of graph statistics, allowing one to quickly and efficiently characterize large graphs. We are also happy to announce that we have released the code for both papers in the Google Research GitHub repository for graph embeddings.

Fully Unsupervised Learning of Graph Similarity
In our 2019 paper, we showed that it is possible to learn representations for graph similarity with neither domain knowledge nor supervision. We propose deep divergence graph kernels (DDGK), an unsupervised method for learning representations over graphs that encode mappings of similarities between them. Unlike previous work, our unsupervised method jointly learns node representations, graph representations, and an attention-based alignment between graphs.
Here is a t-SNE visualization of the latent representations learned by DDGK to compare proteins. Blue points indicate proteins that encode enzymes and the red points are for those that do not. We can see that the encoding correlates with a structural property of the protein (whether or not it encodes enzymes), even though this context was not provided during training. (Note that this is a projection of the representations, and so the absolute axis values aren’t meaningful.)
In the example above, we demonstrate how these representations can automatically learn to represent graphs and align them in a way that encodes their latent functional similarity. Experiments on other datasets show we can capture similarities and differences across graphs of different types (language, biology, and social interactions).
The pairwise distance between different datasets encoded and aligned using DDGK. Color indicates distance in the latent space, and the scale of similarity ranges from 0 (identical) to 1.0 (very different). We see that the representations can be clustered to group similar datasets together — for example, the datasets nci1 and ptc are both datasets of chemical compounds.
Fast and Accurate Approximation of Spectral Descriptors
A graph’s spectrum is a powerful representation that encodes its properties, including connectivity patterns between graph nodes and clustering information. The spectrum has been shown to convey rich information about the properties of different objects such as the sound of a drum, 3D shapes, graphs, and general high-dimensional data. Applications of spectral graph descriptors include AutoML systems, anomaly detection in dynamic graphs, and chemical molecule characterization.

Currently, learning-based systems such as DDGK do not scale to either large graphs or large graph collections. Alternatively, one can use the spectral information without the learning component to attain more desirable scaling properties. However, computing spectral descriptors for large graphs is computationally prohibitive. Our more recent paper addresses this problem by proposing SLaQ, a method for approximating a family of graph descriptors. Our approach uses a randomized approximation algorithm for computing traces of spectrum functions that allows us to study several well-known spectral graph characteristics like Von Neumann Graph Entropy, Estrada Index, graph energy, and NetLSD.

For example, we use SLaQ to monitor anomalous changes in the Wikipedia graph structure. SLaQ allows us to discern meaningful changes in the structure of the page graph from trivial ones such as mass page renames. Our experiments show two orders of magnitude improvement in approximation accuracy, on average.
Left: The well-known Karate graph represents the social interactions of two martial arts clubs. Right: The spectral descriptors (NetLSD, VNGE, and Estrada Index) computed for the original graph in blue and the version with removed edges in red.
Conclusions
Unsupervised representation learning for graphs is an important problem, and we believe that the methods we highlight here are exciting steps forward in this area! Specifically, SLaQ allows us to compute principled representations for vast datasets, and DDGK introduces a mechanism for automatically learning alignments between datasets. We hope that our contributions will help advance the analysis of large datasets, and will be useful for understanding changes to time-varying graph datasets, like those used in recommendation systems.

Acknowledgements
We thank Marina Munkhoeva, Rami Al-Rfou, and Dustin Zelle who contributed to these works. For more information on the Graph Mining team (part of Algorithm and Optimization Group) visit our pages.

Source: Google AI Blog


Innovations in Graph Representation Learning

Posted by Alessandro Epasto, Senior Research Scientist and Bryan Perozzi, Senior Research Scientist, Graph Mining Team

Relational data representing relationships between entities is ubiquitous on the Web (e.g., online social networks) and in the physical world (e.g., in protein interaction networks). Such data can be represented as a graph with nodes (e.g., users, proteins), and edges connecting them (e.g., friendship relations, protein interactions). Given the widespread prevalence of graphs, graph analysis plays a fundamental role in machine learning, with applications in clustering, link prediction, privacy, and others. To apply machine learning methods to graphs (e.g., predicting new friendships, or discovering unknown protein interactions) one needs to learn a representation of the graph that is amenable to be used in ML algorithms.

However, graphs are inherently combinatorial structures made of discrete parts like nodes and edges, while many common ML methods, like neural networks, favor continuous structures, in particular vector representations. Vector representations are particularly important in neural networks, as they can be directly used as input layers. To get around the difficulties in using discrete graph representations in ML, graph embedding methods learn a continuous vector space for the graph, assigning each node (and/or edge) in the graph to a specific position in a vector space. A popular approach in this area is that of random-walk-based representation learning, as introduced in DeepWalk.

Left: The well-known Karate graph representing a social network. Right: A continuous space embedding of the nodes in the graph using DeepWalk.
Here we present the results of two recent papers on graph embedding: “Is a Single Embedding Enough? Learning Node Representations that Capture Multiple Social Contexts” presented at WWW’19 and “Watch Your Step: Learning Node Embeddings via Graph Attention” at NeurIPS’18. The first paper introduces a novel technique to learn multiple embeddings per node, enabling a better characterization of networks with overlapping communities. The second addresses the fundamental problem of hyperparameter tuning in graph embeddings, allowing one to easily deploy graph embeddings methods with less effort. We are also happy to announce that we have released the code for both papers in the Google Research github repository for graph embeddings.

Learning Node Representations that Capture Multiple Social Contexts
In virtually all cases, the crucial assumption of standard graph embedding methods is that a single embedding has to be learned for each node. Thus, the embedding method can be said to seek to identify the single role or position that characterizes each node in the geometry of the graph. Recent work observed, however, that nodes in real networks belong to multiple overlapping communities and play multiple roles—think about your social network where you participate in both your family and in your work community. This observation motivates the following research question: is it possible to develop methods where nodes are embedded in multiple vectors, representing their participation in overlapping communities?

In our WWW’19 paper, we developed Splitter, an unsupervised embedding method that allows the nodes in a graph to have multiple embeddings to better encode their participation in multiple communities. Our method is based on recent innovations in overlapping clustering based on ego-network analysis, using the persona graph concept, in particular. This method takes a graph G, and creates a new graph P (called the persona graph), where each node in G is represented by a series of replicas called the persona nodes. Each persona of a node represents an instantiation of the node in a local community to which it belongs. For each node U in the graph, we analyze the ego-network of the node (i.e., the graph connecting the node to its neighbors, in this example A, B, C, D) to discover local communities to which the node belongs. For instance, in the figure below, node U belongs to two communities: Cluster 1 (with the friends A and B, say U’s family members) and Cluster 2 (with C and D, say U’s colleagues).
Ego-net of node U
Then, we use this information to “split” node U into its two personas U1 (the family persona) and U2 (the work persona). This disentangles the two communities, so that they no longer overlap.
The ego-splitting method separating the U nodes in 2 personas.
This technique has been used to improve the state-of-the-art results in graph embedding methods, showing up to 90% reduction in link prediction (i.e., predicting which link will form in the future) error on a variety of graphs. The key reason for this improvement is the ability of the method to disambiguate highly overlapping communities found in social networks and other real-world graphs. We further validate this result with an in-depth analysis of co-authorship graphs where authors belong to overlapping research communities (e.g., machine learning and data mining).
Top Left: A typical graphs with highly overlapping communities. Top Right: A traditional embedding of the graph on the left using node2vec. Bottom Left: A persona graph of the graph above. Bottom Right: The Splitter embedding of the persona graph. Notice how the persona graph clearly disentangles the overlapping communities of the original graph and Splitter outputs well-separated embeddings.
Automatic hyper-parameter tuning via graph attention.
Graph embedding methods have shown outstanding performance on various ML-based applications, such as link prediction and node classification, but they have a number of hyper-parameters that must be manually set. For example, are nearby nodes more important to capture when learning embeddings than nodes that are further away? Even though experts may be able to fine tune these hyper-parameters, one must do so independently for each graph. To obviate such manual work, in our second paper, we proposed a method to learn the optimal hyper-parameters automatically.

Specifically, many graph embedding methods, like DeepWalk, employ random walks to explore the context around a given node (i.e. the direct neighbors, the neighbors of the neighbors, etc). Such random walks can have many hyper-parameters that allow tuning of the local exploration of the graph, thus regulating the attention given by the embeddings to nearby nodes. Different graphs may present different optimal attention patterns and hence different optimal hyperparameters (see the picture below, where we show two different attention distributions). Watch Your Step formulates a model for the performance of the embedding methods based on the above mentioned hyper-parameters. Then we optimize the hyper-parameters to maximize the performance predicted by the model, using standard backpropagation. We found that the values learned by backpropagation agree with the optimal hyper-parameters obtained by grid search.
Our new method for automatic hyper-parameter tuning, Watch Your Step, uses an attention model to learn different graph context distributions. Shown above are two example local neighborhoods about a center node (in yellow) and the context distributions (red gradient) that was learned by the model. The left-side graph shows a more diffused attention model, while the distribution on the right shows one concentrated on direct neighbors.
This work falls under the growing family of AutoML, where we want to alleviate the burden of optimizing the hyperparameters—a common problem in practical machine learning. Many AutoML methods use neural architecture search. This paper instead shows a variant, where we use the mathematical connection between the hyperparameters in the embeddings and graph-theoretic matrix formulations. The “Auto” portion corresponds to learning the graph hyperparameters by backpropagation.

We believe that our contributions will further advance the state of the research in graph embedding in various directions. Our method for learning multiple node embeddings draws a connection between the rich and well-studied field of overlapping community detection, and the more recent one of graph embedding which we believe may result in fruitful future research. An open problem in this area is the use of multiple-embedding methods for classification. Furthermore, our contribution on learning hyperparameters will foster graph embedding adoption by reducing the need for expensive manual tuning. We hope the release of these papers and code will help the research community pursue these directions.

Acknowledgements
We thank Sami Abu-el-Haija who contributed to this work and is now a Ph.D. student at USC.

Source: Google AI Blog


Coarse Discourse: A Dataset for Understanding Online Discussions

Posted by Praveen Paritosh, Senior Research Scientist, Ka Wong, Senior Data Scientist

Every day, participants of online communities form and share their opinions, experiences, advice and social support, most of which is expressed freely and without much constraint. These online discussions are often a key resource of information for many important topics, such as parenting, fitness, travel and more. However, these discussions also are intermixed with a clutter of disagreements, humor, flame wars and trolling, requiring readers to filter the content before getting the information they are looking for. And while the field of Information Retrieval actively explores ways to allow users to more efficiently find, navigate and consume this content, there is a lack of shared datasets on forum discussions to aid in understanding these discussions a bit better.

To aid researchers in this space, we are releasing the Coarse Discourse dataset, the largest dataset of annotated online discussions to date. The Coarse Discourse contains over half a million human annotations of publicly available online discussions on a random sample of over 9,000 threads from 130 communities from reddit.com.

To create this dataset, we developed the Coarse Discourse taxonomy of forum comments by going through a small set of forum threads, reading every comment, and deciding what role the comments played in the discussion. We then repeated and revised this exercise with crowdsourced human editors to validate the reproducibility of the taxonomy's discourse types, which include: announcement, question, answer, agreement, disagreement, appreciation, negative reaction, elaboration, and humor. From this data, over 100,000 comments were independently annotated by the crowdsourced editors for discourse type and relation. Along with the raw annotations from crowdsourced editors, we also provide the Coarse Discourse annotation task guidelines used by the editors to help with collecting data for other forums and refining the task further.
An example thread annotated with discourse types and relations. Early findings suggest that question answering is a prominent use case in most communities, while some communities are more converationally focused, with back-and-forth interactions.
For machine learning and natural language processing researchers trying to characterize the nature of online discussions, we hope that this dataset is a useful resource. Visit our GitHub repository to download the data. For more details, check out our ICWSM paper, “Characterizing Online Discussion Using Coarse Discourse Sequences.”

Acknowledgments
This work was done by Amy Zhang during her internship at Google. We would also like to thank Bryan Culbertson, Olivia Rhinehart, Eric Altendorf, David Huynh, Nancy Chang, Chris Welty and our crowdsourced editors.

Research from VLDB 2016: Improved Friend Suggestion using Ego-Net Analysis

Posted by Alessandro Epasto, Research Scientist, Google Research NY

On September 5 - 9, New Delhi, India hosted the 42nd International Conference on Very Large Data Bases (VLDB), a premier annual forum for academic and industry research on databases, data management, data mining and data analytics. Over the past several years, Google has actively participated in VLDB, both as official sponsor and with numerous contributions to the research and industrial tracks. In this post, we would like to share the research presented in one of the Google papers from VLDB 2016.

In Ego-net Community Mining Applied to Friend Suggestion, co-authored by Googlers Silvio Lattanzi, Vahab Mirrokni, Ismail Oner Sebe, Ahmed Taei, Sunita Verma and myself, we explore how social networks can provide better friend suggestions to users, a challenging practical problem faced by all social network platforms

Friend suggestion – the task of suggesting to a user the contacts she might already know in the network but that she hasn’t added yet – is major driver of user engagement and social connection in all online social networks. Designing a high quality system that can provide relevant and useful friend recommendations is very challenging, and requires state-of-the-art machine learning algorithms based on a multitude of parameters.

An effective family of features for friend suggestion consist of graph features such as the number of common friends between two users. While widely used, the number of common friends has some major drawbacks, including the following which is shown in Figure 1.
Figure 1: Ego-net of Sally.
In this figure we represent the social connections of Sally and her friends – the ego-net of Sally. An ego-net of a node (in this case, Sally) is defined as the graph that contains the node itself, all of the node’s neighbors and the connection among those nodes. Sally has 6 friends in her ego-net: Albert (her husband), Brian (her son), Charlotte (her mother) as well as Uma (her boss), Vincent and Wally (two of her team members). Notice how A, B and C are all connected with each other while they do not know U, V or W. On the other hand U, V and W have all added each other as their friend (except U and W who are good friend but somehow forgot to add each other).

Notice how each of A, B, C have a common friend with each of U, V and W: Sally herself. A friend recommendation system based on common neighbors might suggest to Sally’s son (for instance) to add Sally’s boss as his friend! In reality the situation is even more complicated because users’ online and offline friends span several different social circles or communities (family, work, school, sports, etc).

In our paper we introduce a novel technique for friend suggestions based on independently analyzing the ego-net structure. The main contribution of the paper is to show that it is possible to provide friend suggestions efficiently by constructing all ego-nets of the nodes in the graph and then independently applying community detection algorithms on them in large-scale distributed systems.

Specifically, the algorithm proceeds by constructing the ego-nets of all nodes and applying, independently on each of them, a community detection algorithm. More precisely the algorithm operates on so-called “ego-net-minus-ego” graphs, which is defined as the graph including only the neighbors of a given node, as shown in the figure below.
Figure 2: Clustering of the ego-net of Sally.
Notice how in this example the ego-net-minus-ego of Sally has two very clear communities: her family (A, B, C) and her co-workers (U, V, W) which are easily separated. Intuitively, this is because one might expect that while nodes (e.g. Sally) participate in many communities, there is usually a single (or a limited number of) contexts in which two specific neighbors interact. While Sally is both part of her family and work community, Sally and Uma interact only at work. Through extensive experimental evaluation on large-scale public social networks and formally through a simple mathematical model, our paper confirms this intuition. It seems that while communities are hard to separate in a global graph, they are easier to identify at the local level of ego-nets.

This allows for a novel graph-based method for friend suggestion which intuitively only allows suggestion of pairs of users that are clustered together in the same community from the point of view of their common friends. With this method, U and W will be suggested to add each other (as they are in the same community and they are not yet connected) while B and U will not be suggested as friends as they span two different communities.

From an algorithmic point of view, the paper introduces efficient parallel and distributed techniques for computing and clustering all ego-nets of very large graphs at the same time – a fundamental aspect enabling use of the system on the entire world Google+ graph. We have applied this feature in the “You May Know” system of Google+, resulting in a clear positive impact on the prediction task, improving the acceptance rate by more than 1.5% and decreasing the rejection rate by more than 3.3% (a significative impact at Google scales).

We believe that many future directions of work might stem from our preliminary results. For instance ego-net analysis could be potentially to automatically classify a user contacts in circles and to detect spam. Another interesting direction is the study of ego-network evolution in dynamic graphs.