 Posted by Mayank Jain – Product Manager and Jomo Fisher – Software Engineer
Posted by Mayank Jain – Product Manager and Jomo Fisher – Software Engineer
Get ready to upgrade your app's performance as Android embraces 16 KB memory page sizes
Android’s transition to 16 KB Page size
Traditionally, Android has operated with the 4 KB memory page size. However many ARM CPUs (the most common processors for Android phones) support the larger 16 KB page size, offering improved performance gains. With Android 15, the Android operating system is page-size-agnostic, allowing devices to run efficiently with either 4 KB or 16 KB page size.
Starting November 1st, 2025, all new apps and app updates that use native C/C++ code targeting Android 15+ devices submitted to Google Play must support 16 KB page sizes. This is a crucial step towards ensuring your app delivers the best possible performance on the latest Android hardware. Apps without native C/C++ code or dependencies, that just use the Kotlin and Java programming languages, are already compatible, but if you're using native code, now is the time to act.
This transition to larger 16 KB page sizes translates directly into a better user experience. Devices configured with 16 KB page size can see an overall performance boost of 5-10%. This means faster app launch times (up to 30% for some apps, 3.16% on average), improved battery usage (4.56% reduction in power draw), quicker camera starts (4.48-6.60% faster), and even speedier system boot-ups (around 0.8 seconds faster). While there is a marginal increase in memory use, a faster reclaim path is worth it.
The native code challenge – and how Android Studio equips you
If your app uses native C/C++ code from the Android NDK or relies on SDKs that do, you'll need to recompile and potentially adjust your code for 16 KB compatibility. The good news? Once your application is updated for the 16 KB page size, the same application binary can run seamlessly on both 4 KB and 16 KB devices.
This table describes who needs to transition and recompile their apps
We’ve created several Android Studio tools and guides that can help you prepare for migrating to using 16 KB page size.
Detect compatibility issues
APK Analyzer: Easily identify if your app contains native libraries by checking for .so files in the lib folder. The APK Analyzer can also visually indicate your app's 16 KB compatibility. You can then determine and update libraries as needed for 16 KB compliance.
Alignment Checks: Android Studio also provides warnings if your prebuilt libraries or APKs are not 16 KB compliant. You should then use the APK Analyzer tool to review which libraries need to be updated or if any code changes are required. If you want to detect the 16 KB page size compatibility checks in your CI (continuous integration) pipeline, you can leverage scripts and command line tools.
Lint in Android Studio now also highlights the native libraries which are not 16 KB aligned.
Build with 16 KB alignment
Tools Updates: Rebuild your native code with 16 KB alignment. Android Gradle Plugin (AGP) version 8.5.1 or higher automatically enables 16 KB alignment by default (during packaging) for uncompressed shared libraries. Similarly, Android NDK r28 and higher compile 16 KB-aligned by default. If you depend on other native SDK’s, they also need to be 16 KB aligned. You might need to reach out to the SDK developer to request a 16 KB compliant SDK.
Fix code for page-size agnosticism
Eliminate Hardcoded Assumptions: Identify and remove any hardcoded dependencies on PAGE_SIZE or assumptions that the page size is 4 KB (e.g., 4096). Instead, use getpagesize() or sysconf(_SC_PAGESIZE) to query the actual page size at runtime.
Test in a 16 KB environment
Android Emulator Support: Android Studio offers a 16 KB emulator target (for both arm64 and x86_64) directly in the Android Studio SDK Manager, allowing you to test your applications before uploading to Google Play.
On-Device Testing: For compatible devices like Pixel 8 and 8 Pro onwards (starting with Android 15 QPR1), a new developer option allows you to switch between 4 KB and 16 KB page sizes for real-device testing. You can verify the page size using adb shell getconf PAGE_SIZE.
Don't wait – prepare your apps today
Leverage Android Studio’s powerful tools to detect issues, build compatible binaries, fix your code, and thoroughly test your app for the new 16 KB memory page sizes. By doing so, you'll ensure an improved end user experience and contribute to a more performant Android ecosystem.
As always, your feedback is important to us – check known issues, report bugs, suggest improvements, and be part of our vibrant community on LinkedIn, Medium, YouTube, or X.
 Posted by Mayank Jain – Product Manager and Jomo Fisher – Software Engineer
Posted by Mayank Jain – Product Manager and Jomo Fisher – Software Engineer





 Posted by Dan Galpin – Android Developer Relations
Posted by Dan Galpin – Android Developer Relations


 Posted by J. Eason – Director, Product Management
Posted by J. Eason – Director, Product Management



 Tens of millions of videos have been generated in Flow, our AI tool for filmmakers since launching in May.To help get the most out of Flow, starting this week, you can a…
Tens of millions of videos have been generated in Flow, our AI tool for filmmakers since launching in May.To help get the most out of Flow, starting this week, you can a…
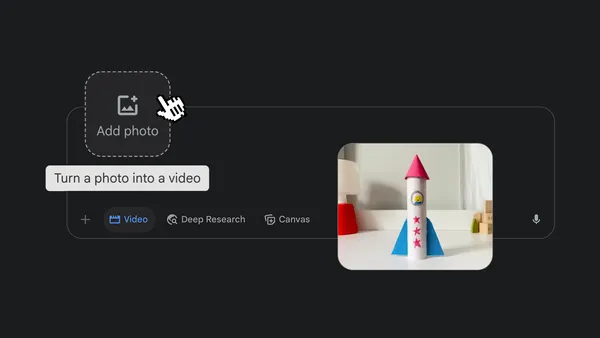 You can now use Veo 3 to create video clips from photos you upload in the Gemini app.
You can now use Veo 3 to create video clips from photos you upload in the Gemini app.
