Tag Archives: DeepMind

AdaTape: Foundation model with adaptive computation and dynamic read-and-write

Posted by Fuzhao Xue, Research Intern, and Mostafa Dehghani, Research Scientist, Google

Adaptive computation refers to the ability of a machine learning system to adjust its behavior in response to changes in the environment. While conventional neural networks have a fixed function and computation capacity, i.e., they spend the same number of FLOPs for processing different inputs, a model with adaptive and dynamic computation modulates the computational budget it dedicates to processing each input, depending on the complexity of the input.

Adaptive computation in neural networks is appealing for two key reasons. First, the mechanism that introduces adaptivity provides an inductive bias that can play a key role in solving some challenging tasks. For instance, enabling different numbers of computational steps for different inputs can be crucial in solving arithmetic problems that require modeling hierarchies of different depths. Second, it gives practitioners the ability to tune the cost of inference through greater flexibility offered by dynamic computation, as these models can be adjusted to spend more FLOPs processing a new input.

Neural networks can be made adaptive by using different functions or computation budgets for various inputs. A deep neural network can be thought of as a function that outputs a result based on both the input and its parameters. To implement adaptive function types, a subset of parameters are selectively activated based on the input, a process referred to as conditional computation. Adaptivity based on the function type has been explored in studies on mixture-of-experts, where the sparsely activated parameters for each input sample are determined through routing.

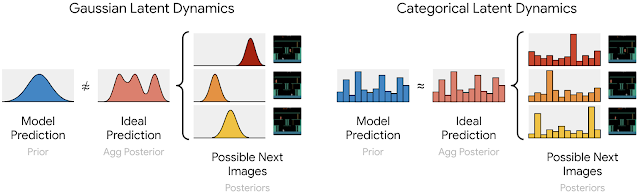
Another area of research in adaptive computation involves dynamic computation budgets. Unlike in standard neural networks, such as T5, GPT-3, PaLM, and ViT, whose computation budget is fixed for different samples, recent research has demonstrated that adaptive computation budgets can improve performance on tasks where transformers fall short. Many of these works achieve adaptivity by using dynamic depth to allocate the computation budget. For example, the Adaptive Computation Time (ACT) algorithm was proposed to provide an adaptive computational budget for recurrent neural networks. The Universal Transformer extends the ACT algorithm to transformers by making the computation budget dependent on the number of transformer layers used for each input example or token. Recent studies, like PonderNet, follow a similar approach while improving the dynamic halting mechanisms.

In the paper “Adaptive Computation with Elastic Input Sequence”, we introduce a new model that utilizes adaptive computation, called AdaTape. This model is a Transformer-based architecture that uses a dynamic set of tokens to create elastic input sequences, providing a unique perspective on adaptivity in comparison to previous works. AdaTape uses an adaptive tape reading mechanism to determine a varying number of tape tokens that are added to each input based on input’s complexity. AdaTape is very simple to implement, provides an effective knob to increase the accuracy when needed, but is also much more efficient compared to other adaptive baselines because it directly injects adaptivity into the input sequence instead of the model depth. Finally, Adatape offers better performance on standard tasks, like image classification, as well as algorithmic tasks, while maintaining a favorable quality and cost tradeoff.


Adaptive computation transformer with elastic input sequence

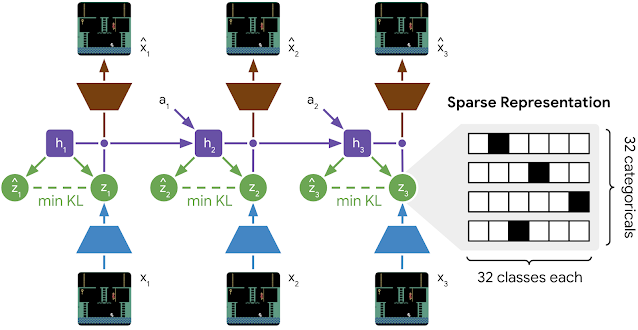
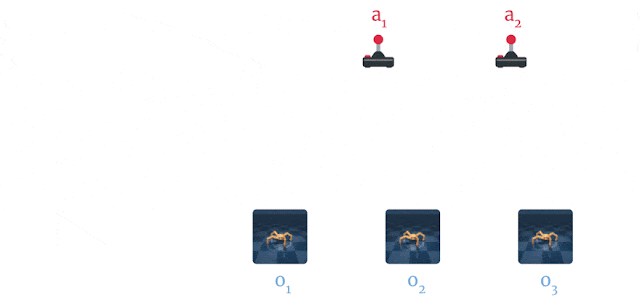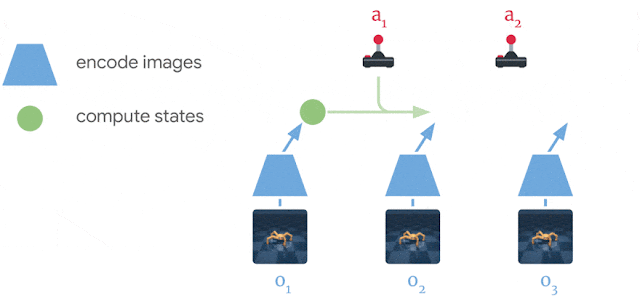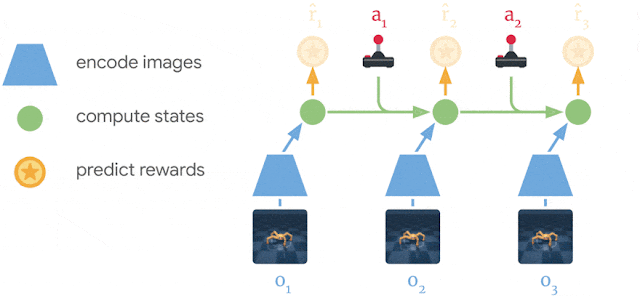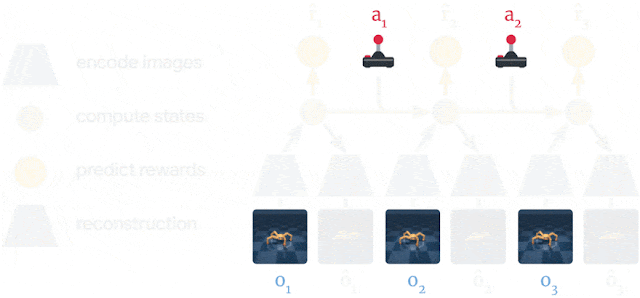
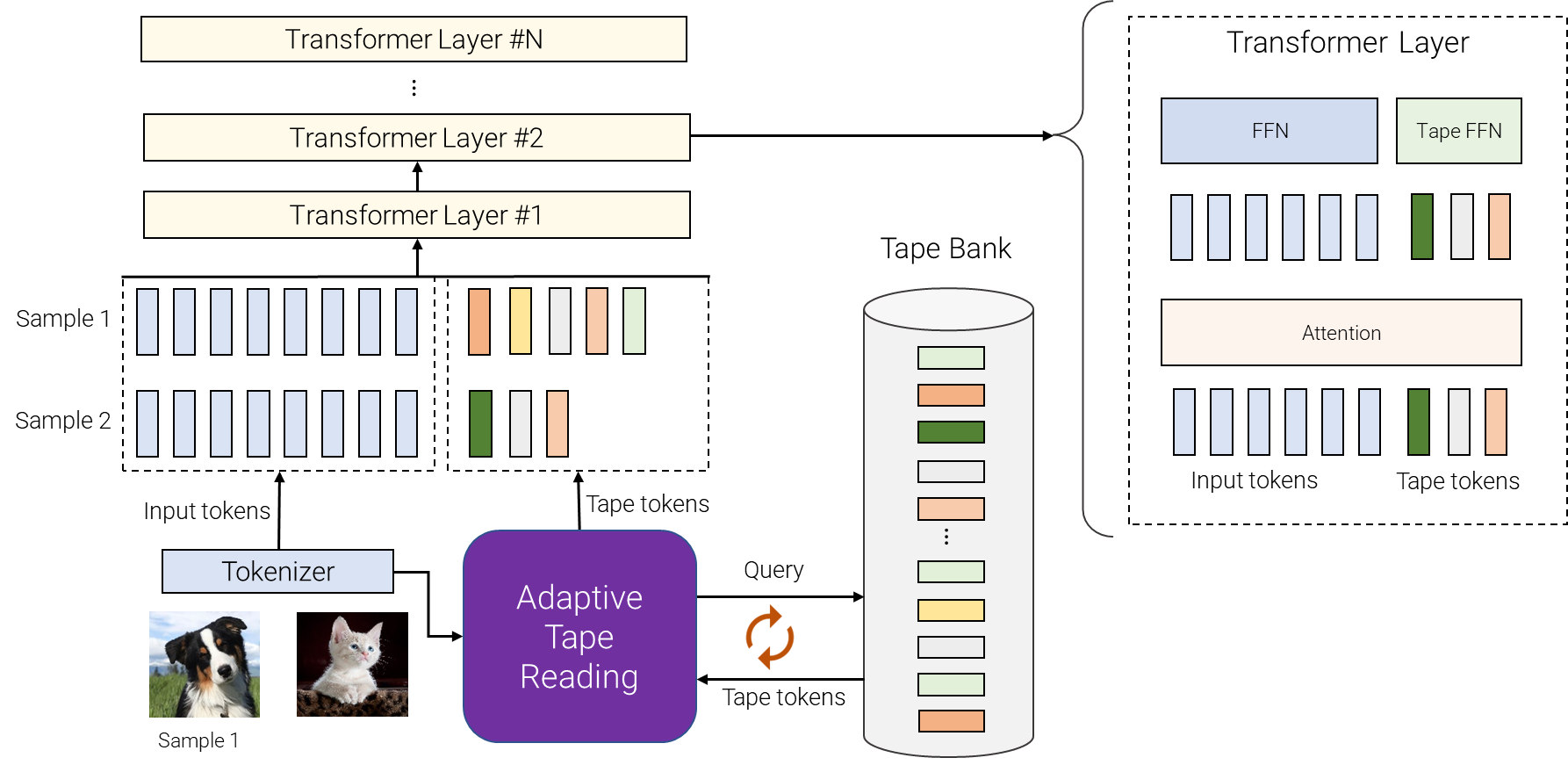
AdaTape uses both the adaptive function types and a dynamic computation budget. Specifically, for a batch of input sequences after tokenization (e.g., a linear projection of non-overlapping patches from an image in the vision transformer), AdaTape uses a vector representing each input to dynamically select a variable-sized sequence of tape tokens.

AdaTape uses a bank of tokens, called a “tape bank”, to store all the candidate tape tokens that interact with the model through the adaptive tape reading mechanism. We explore two different methods for creating the tape bank: an input-driven bank and a learnable bank.

The general idea of the input-driven bank is to extract a bank of tokens from the input while employing a different approach than the original model tokenizer for mapping the raw input to a sequence of input tokens. This enables dynamic, on-demand access to information from the input that is obtained using a different point of view, e.g., a different image resolution or a different level of abstraction.

In some cases, tokenization in a different level of abstraction is not possible, thus an input-driven tape bank is not feasible, such as when it's difficult to further split each node in a graph transformer. To address this issue, AdaTape offers a more general approach for generating the tape bank by using a set of trainable vectors as tape tokens. This approach is referred to as the learnable bank and can be viewed as an embedding layer where the model can dynamically retrieve tokens based on the complexity of the input example. The learnable bank enables AdaTape to generate a more flexible tape bank, providing it with the ability to dynamically adjust its computation budget based on the complexity of each input example, e.g., more complex examples retrieve more tokens from the bank, which let the model not only use the knowledge stored in the bank, but also spend more FLOPs processing it, since the input is now larger.

Finally, the selected tape tokens are appended to the original input and fed to the following transformer layers. For each transformer layer, the same multi-head attention is used across all input and tape tokens. However, two different feed-forward networks (FFN) are used: one for all tokens from the original input and the other for all tape tokens. We observed slightly better quality by using separate feed-forward networks for input and tape tokens.

An overview of AdaTape. For different samples, we pick a variable number of different tokens from the tape bank. The tape bank can be driven from input, e.g., by extracting some extra fine-grained information or it can be a set of trainable vectors. Adaptive tape reading is used to recursively select different sequences of tape tokens, with variable lengths, for different inputs. These tokens are then simply appended to inputs and fed to the transformer encoder.

AdaTape provides helpful inductive bias

We evaluate AdaTape on parity, a very challenging task for the standard Transformer, to study the effect of inductive biases in AdaTape. With the parity task, given a sequence 1s, 0s, and -1s, the model has to predict the evenness or oddness of the number of 1s in the sequence. Parity is the simplest non-counter-free or periodic regular language, but perhaps surprisingly, the task is unsolvable by the standard Transformer.

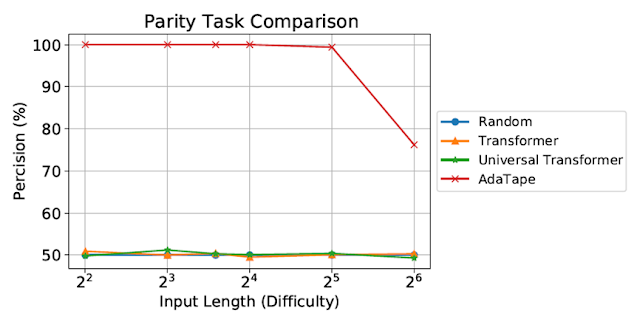Evaluation on the parity task. The standard Transformer and Universal Transformer were unable to perform this task, both showing performance at the level of a random guessing baseline.

Despite being evaluated on short, simple sequences, both the standard Transformer and Universal Transformers were unable to perform the parity task as they are unable to maintain a counter within the model. However, AdaTape outperforms all baselines, as it incorporates a lightweight recurrence within its input selection mechanism, providing an inductive bias that enables the implicit maintenance of a counter, which is not possible in standard Transformers.


Evaluation on image classification

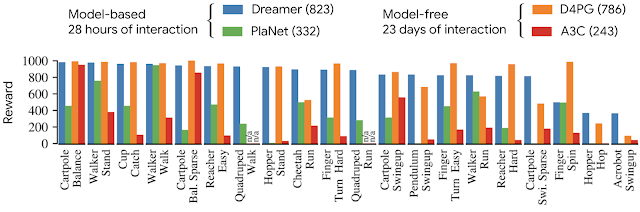
We also evaluate AdaTape on the image classification task. To do so, we trained AdaTape on ImageNet-1K from scratch. The figure below shows the accuracy of AdaTape and the baseline methods, including A-ViT, and the Universal Transformer ViT (UViT and U2T) versus their speed (measured as number of images, processed by each code, per second). In terms of quality and cost tradeoff, AdaTape performs much better than the alternative adaptive transformer baselines. In terms of efficiency, larger AdaTape models (in terms of parameter count) are faster than smaller baselines. Such results are consistent with the finding from previous work that shows that the adaptive model depth architectures are not well suited for many accelerators, like the TPU.

We evaluate AdaTape by training on ImageNet from scratch. For A-ViT, we not only report their results from the paper but also re-implement A-ViT by training from scratch, i.e., A-ViT(Ours).

A study of AdaTape’s behavior

In addition to its performance on the parity task and ImageNet-1K, we also evaluated the token selection behavior of AdaTape with an input-driven bank on the JFT-300M validation set. To better understand the model's behavior, we visualized the token selection results on the input-driven bank as heatmaps, where lighter colors mean that position is more frequently selected. The heatmaps reveal that AdaTape more frequently picks the central patches. This aligns with our prior knowledge, as central patches are typically more informative — especially in the context of datasets with natural images, where the main object is in the middle of the image. This result highlights the intelligence of AdaTape, as it can effectively identify and prioritize more informative patches to improve its performance.

We visualize the tape token selection heatmap of AdaTape-B/32 (left) and AdaTape-B/16 (right). The hotter / lighter color means the patch at this position is more frequently selected.

Conclusion

AdaTape is characterized by elastic sequence lengths generated by the adaptive tape reading mechanism. This also introduces a new inductive bias that enables AdaTape to have the potential to solve tasks that are challenging for both standard transformers and existing adaptive transformers. By conducting comprehensive experiments on image recognition benchmarks, we demonstrate that AdaTape outperforms standard transformers and adaptive architecture transformers when computation is held constant.


Acknowledgments

One of the authors of this post, Mostafa Dehghani, is now at Google DeepMind.

Source: Google AI Blog


Resolving code review comments with ML

Posted by Alexander Frömmgen, Staff Software Engineer, and Lera Kharatyan, Senior Software Engineer, Core Systems & Experiences

Code-change reviews are a critical part of the software development process at scale, taking a significant amount of the code authors’ and the code reviewers’ time. As part of this process, the reviewer inspects the proposed code and asks the author for code changes through comments written in natural language. At Google, we see millions of reviewer comments per year, and authors require an average of ~60 minutes active shepherding time between sending changes for review and finally submitting the change. In our measurements, the required active work time that the code author must do to address reviewer comments grows almost linearly with the number of comments. However, with machine learning (ML), we have an opportunity to automate and streamline the code review process, e.g., by proposing code changes based on a comment’s text.

Today, we describe applying recent advances of large sequence models in a real-world setting to automatically resolve code review comments in the day-to-day development workflow at Google (publication forthcoming). As of today, code-change authors at Google address a substantial amount of reviewer comments by applying an ML-suggested edit. We expect that to reduce time spent on code reviews by hundreds of thousands of hours annually at Google scale. Unsolicited, very positive feedback highlights that the impact of ML-suggested code edits increases Googlers' productivity and allows them to focus on more creative and complex tasks.


Predicting the code edit

We started by training a model that predicts code edits needed to address reviewer comments. The model is pre-trained on various coding tasks and related developer activities (e.g., renaming a variable, repairing a broken build, editing a file). It’s then fine-tuned for this specific task with reviewed code changes, the reviewer comments, and the edits the author performed to address those comments.

An example of an ML-suggested edit of refactorings that are spread within the code.

Google uses a monorepo, a single repository for all of its software artifacts, which allows our training dataset to include all unrestricted code used to build Google's most recent software, as well as previous versions.

To improve the model quality, we iterated on the training dataset. For example, we compared the model performance for datasets with a single reviewer comment per file to datasets with multiple comments per file, and experimented with classifiers to clean up the training data based on a small, curated dataset to choose the model with the best offline precision and recall metrics.


Serving infrastructure and user experience

We designed and implemented the feature on top of the trained model, focusing on the overall user experience and developer efficiency. As part of this, we explored different user experience (UX) alternatives through a series of user studies. We then refined the feature based on insights from an internal beta (i.e., a test of the feature in development) including user feedback (e.g., a “Was this helpful?” button next to the suggested edit).

The final model was calibrated for a target precision of 50%. That is, we tuned the model and the suggestions filtering, so that 50% of suggested edits on our evaluation dataset are correct. In general, increasing the target precision reduces the number of shown suggested edits, and decreasing the target precision leads to more incorrect suggested edits. Incorrect suggested edits take the developers time and reduce the developers’ trust in the feature. We found that a target precision of 50% provides a good balance.

At a high level, for every new reviewer comment, we generate the model input in the same format that is used for training, query the model, and generate the suggested code edit. If the model is confident in the prediction and a few additional heuristics are satisfied, we send the suggested edit to downstream systems. The downstream systems, i.e., the code review frontend and the integrated development environment (IDE), expose the suggested edits to the user and log user interactions, such as preview and apply events. A dedicated pipeline collects these logs and generates aggregate insights, e.g., the overall acceptance rates as reported in this blog post.

Architecture of the ML-suggested edits infrastructure. We process code and infrastructure from multiple services, get the model predictions and surface the predictions in the code review tool and IDE.

The developer interacts with the ML-suggested edits in the code review tool and the IDE. Based on insights from the user studies, the integration into the code review tool is most suitable for a streamlined review experience. The IDE integration provides additional functionality and supports 3-way merging of the ML-suggested edits (left in the figure below) in case of conflicting local changes on top of the reviewed code state (right) into the merge result (center).

3-way-merge UX in IDE.

Results

Offline evaluations indicate that the model addresses 52% of comments with a target precision of 50%. The online metrics of the beta and the full internal launch confirm these offline metrics, i.e., we see model suggestions above our target model confidence for around 50% of all relevant reviewer comments. 40% to 50% of all previewed suggested edits are applied by code authors.

We used the “not helpful” feedback during the beta to identify recurring failure patterns of the model. We implemented serving-time heuristics to filter these and, thus, reduce the number of shown incorrect predictions. With these changes, we traded quantity for quality and observed an increased real-world acceptance rate.

Code review tool UX. The suggestion is shown as part of the comment and can be previewed, applied and rated as helpful or not helpful.

Our beta launch showed a discoverability challenge: code authors only previewed ~20% of all generated suggested edits. We modified the UX and introduced a prominent “Show ML-edit” button (see the figure above) next to the reviewer comment, leading to an overall preview rate of ~40% at launch. We additionally found that suggested edits in the code review tool are often not applicable due to conflicting changes that the author did during the review process. We addressed this with a button in the code review tool that opens the IDE in a merge view for the suggested edit. We now observe that more than 70% of these are applied in the code review tool and fewer than 30% are applied in the IDE. All these changes allowed us to increase the overall fraction of reviewer comments that are addressed with an ML-suggested edit by a factor of 2 from beta to the full internal launch. At Google scale, these results help automate the resolution of hundreds of thousands of comments each year.

Suggestions filtering funnel.

We see ML-suggested edits addressing a wide range of reviewer comments in production. This includes simple localized refactorings and refactorings that are spread within the code, as shown in the examples throughout the blog post above. The feature addresses longer and less formally-worded comments that require code generation, refactorings and imports.

Example of a suggestion for a longer and less formally worded comment that requires code generation, refactorings and imports.

The model can also respond to complex comments and produce extensive code edits (shown below). The generated test case follows the existing unit test pattern, while changing the details as described in the comment. Additionally, the edit suggests a comprehensive name for the test reflecting the test semantics.

Example of the model's ability to respond to complex comments and produce extensive code edits.

Conclusion and future work

In this post, we introduced an ML-assistance feature to reduce the time spent on code review related changes. At the moment, a substantial amount of all actionable code review comments on supported languages are addressed with applied ML-suggested edits at Google. A 12-week A/B experiment across all Google developers will further measure the impact of the feature on the overall developer productivity.

We are working on improvements throughout the whole stack. This includes increasing the quality and recall of the model and building a more streamlined experience for the developer with improved discoverability throughout the review process. As part of this, we are investigating the option of showing suggested edits to the reviewer while they draft comments and expanding the feature into the IDE to enable code-change authors to get suggested code edits for natural-language commands.


Acknowledgements

This is the work of many people in Google Core Systems & Experiences team, Google Research, and DeepMind. We'd like to specifically thank Peter Choy for bringing the collaboration together, and all of our team members for their key contributions and useful advice, including Marcus Revaj, Gabriela Surita, Maxim Tabachnyk, Jacob Austin, Nimesh Ghelani, Dan Zheng, Peter Josling, Mariana Stariolo, Chris Gorgolewski, Sascha Varkevisser, Katja Grünwedel, Alberto Elizondo, Tobias Welp, Paige Bailey, Pierre-Antoine Manzagol, Pascal Lamblin, Chenjie Gu, Petros Maniatis, Henryk Michalewski, Sara Wiltberger, Ambar Murillo, Satish Chandra, Madhura Dudhgaonkar, Niranjan Tulpule, Zoubin Ghahramani, Juanjo Carin, Danny Tarlow, Kevin Villela, Stoyan Nikolov, David Tattersall, Boris Bokowski, Kathy Nix, Mehdi Ghissassi, Luis C. Cobo, Yujia Li, David Choi, Kristóf Molnár, Vahid Meimand, Amit Patel, Brett Wiltshire, Laurent Le Brun, Mingpan Guo, Hermann Loose, Jonas Mattes, Savinee Dancs.

Source: Google AI Blog


OptFormer: Towards Universal Hyperparameter Optimization with Transformers

Posted by Yutian Chen, Staff Research Scientist, DeepMind, and Xingyou (Richard) Song, Research Scientist, Google Research, Brain Team

One of the most important aspects in machine learning is hyperparameter optimization, as finding the right hyperparameters for a machine learning task can make or break a model’s performance. Internally, we regularly use Google Vizier as the default platform for hyperparameter optimization. Throughout its deployment over the last 5 years, Google Vizier has been used more than 10 million times, over a vast class of applications, including machine learning applications from vision, reinforcement learning, and language but also scientific applications such as protein discovery and hardware acceleration. As Google Vizier is able to keep track of use patterns in its database, such data, usually consisting of optimization trajectories termed studies, contain very valuable prior information on realistic hyperparameter tuning objectives, and are thus highly attractive for developing better algorithms.

While there have been many previous methods for meta-learning over such data, such methods share one major common drawback: their meta-learning procedures depend heavily on numerical constraints such as the number of hyperparameters and their value ranges, and thus require all tasks to use the exact same total hyperparameter search space (i.e., tuning specifications). Additional textual information in the study, such as its description and parameter names, are also rarely used, yet can hold meaningful information about the type of task being optimized. Such a drawback becomes more exacerbated for larger datasets, which often contain significant amounts of such meaningful information.

Today in “Towards Learning Universal Hyperparameter Optimizers with Transformers”, we are excited to introduce the OptFormer, one of the first Transformer-based frameworks for hyperparameter tuning, learned from large-scale optimization data using flexible text-based representations. While numerous works have previously demonstrated the Transformer’s strong abilities across various domains, few have touched on its optimization-based capabilities, especially over text space. Our core findings demonstrate for the first time some intriguing algorithmic abilities of Transformers: 1) a single Transformer network is capable of imitating highly complex behaviors from multiple algorithms over long horizons; 2) the network is further capable of predicting objective values very accurately, in many cases surpassing Gaussian Processes, which are commonly used in algorithms such as Bayesian Optimization.

Approach: Representing Studies as Tokens
Rather than only using numerical data as common with previous methods, our novel approach instead utilizes concepts from natural language and represents all of the study data as a sequence of tokens, including textual information from initial metadata. In the animation below, this includes “CIFAR10”, “learning rate”, “optimizer type”, and “Accuracy”, which informs the OptFormer of an image classification task. The OptFormer then generates new hyperparameters to try on the task, predicts the task accuracy, and finally receives the true accuracy, which will be used to generate the next round’s hyperparameters. Using the T5X codebase, the OptFormer is trained in a typical encoder-decoder fashion using standard generative pretraining over a wide range of hyperparameter optimization objectives, including real world data collected by Google Vizier, as well as public hyperparameter (HPO-B) and blackbox optimization benchmarks (BBOB).

The OptFormer can perform hyperparameter optimization encoder-decoder style, using token-based representations. It initially observes text-based metadata (in the gray box) containing information such as the title, search space parameter names, and metrics to optimize, and repeatedly outputs parameter and objective value predictions.

Imitating Policies
As the OptFormer is trained over optimization trajectories by various algorithms, it may now accurately imitate such algorithms simultaneously. By providing a text-based prompt in the metadata for the designated algorithm (e.g. “Regularized Evolution”), the OptFormer will imitate the algorithm’s behavior.

Over an unseen test function, the OptFormer produces nearly identical optimization curves as the original algorithm. Mean and standard deviation error bars are shown.

Predicting Objective Values
In addition, the OptFormer may now predict the objective value being optimized (e.g. accuracy) and provide uncertainty estimates. We compared the OptFormer’s prediction with a standard Gaussian Process and found that the OptFormer was able to make significantly more accurate predictions. This can be seen below qualitatively, where the OptFormer’s calibration curve closely follows the ideal diagonal line in a goodness-of-fit test, and quantitatively through standard aggregate metrics such as log predictive density.

Left: Rosenblatt Goodness-of-Fit. Closer diagonal fit is better. Right: Log Predictive Density. Higher is better.

Combining Both: Model-based Optimization
We may now use the OptFormer’s function prediction capability to better guide our imitated policy, similar to techniques found in Bayesian Optimization. Using Thompson Sampling, we may rank our imitated policy’s suggestions and only select the best according to the function predictor. This produces an augmented policy capable of outperforming our industry-grade Bayesian Optimization algorithm in Google Vizier when optimizing classic synthetic benchmark objectives and tuning the learning rate hyperparameters of a standard CIFAR-10 training pipeline.

Left: Best-so-far optimization curve over a classic Rosenbrock function. Right: Best-so-far optimization curve over hyperparameters for training a ResNet-50 on CIFAR-10 via init2winit. Both cases use 10 seeds per curve, and error bars at 25th and 75th percentiles.

Conclusion
Throughout this work, we discovered some useful and previously unknown optimization capabilities of the Transformer. In the future, we hope to pave the way for a universal hyperparameter and blackbox optimization interface to use both numerical and textual data to facilitate optimization over complex search spaces, and integrate the OptFormer with the rest of the Transformer ecosystem (e.g. language, vision, code) by leveraging Google’s vast collection of offline AutoML data.

Acknowledgements
The following members of DeepMind and the Google Research Brain Team conducted this research: Yutian Chen, Xingyou Song, Chansoo Lee, Zi Wang, Qiuyi Zhang, David Dohan, Kazuya Kawakami, Greg Kochanski, Arnaud Doucet, Marc'aurelio Ranzato, Sagi Perel, and Nando de Freitas.

We would like to also thank Chris Dyer, Luke Metz, Kevin Murphy, Yannis Assael, Frank Hutter, and Esteban Real for providing valuable feedback, and further thank Sebastian Pineda Arango, Christof Angermueller, and Zachary Nado for technical discussions on benchmarks. In addition, we thank Daniel Golovin, Daiyi Peng, Yingjie Miao, Jack Parker-Holder, Jie Tan, Lucio Dery, and Aleksandra Faust for multiple useful conversations.

Finally, we thank Tom Small for designing the animation for this post.

Source: Google AI Blog


Mastering Atari with Discrete World Models

Posted by Danijar Hafner, Student Researcher, Google Research

Deep reinforcement learning (RL) enables artificial agents to improve their decisions over time. Traditional model-free approaches learn which of the actions are successful in different situations by interacting with the environment through a large amount of trial and error. In contrast, recent advances in deep RL have enabled model-based approaches to learn accurate world models from image inputs and use them for planning. World models can learn from fewer interactions, facilitate generalization from offline data, enable forward-looking exploration, and allow reusing knowledge across multiple tasks.

Despite their intriguing benefits, existing world models (such as SimPLe) have not been accurate enough to compete with the top model-free approaches on the most competitive reinforcement learning benchmarks — to date, the well-established Atari benchmark requires model-free algorithms, such as DQN, IQN, and Rainbow, to reach human-level performance. As a result, many researchers have focused instead on developing task-specific planning methods, such as VPN and MuZero, which learn by predicting sums of expected task rewards. However, these methods are specific to individual tasks and it is unclear how well they would generalize to new tasks or learn from unsupervised datasets. Similar to the recent breakthrough of unsupervised representation learning in computer vision [1, 2], world models aim to learn patterns in the environment that are more general than any particular task to later solve tasks more efficiently.

Today, in collaboration with DeepMind and the University of Toronto, we introduce DreamerV2, the first RL agent based on a world model to achieve human-level performance on the Atari benchmark. It constitutes the second generation of the Dreamer agent that learns behaviors purely within the latent space of a world model trained from pixels. DreamerV2 relies exclusively on general information from the images and accurately predicts future task rewards even when its representations were not influenced by those rewards. Using a single GPU, DreamerV2 outperforms top model-free algorithms with the same compute and sample budget.

Gamer normalized median score across the 55 Atari games after 200 million steps. DreamerV2 substantially outperforms previous world models. Moreover, it exceeds top model-free agents within the same compute and sample budget.
Behaviors learned by DreamerV2 for some of the 55 Atari games. These videos show images from the environment. Video predictions are shown below in the blog post.

An Abstract Model of the World
Just like its predecessor, DreamerV2 learns a world model and uses it to train actor-critic behaviors purely from predicted trajectories. The world model automatically learns to compute compact representations of its images that discover useful concepts, such as object positions, and learns how these concepts change in response to different actions. This lets the agent generate abstractions of its images that ignore irrelevant details and enables massively parallel predictions on a single GPU. During 200 million environment steps, DreamerV2 predicts 468 billion compact states for learning its behavior.

DreamerV2 builds upon the Recurrent State-Space Model (RSSM) that we introduced for PlaNet and was also used for DreamerV1. During training, an encoder turns each image into a stochastic representation that is incorporated into the recurrent state of the world model. Because the representations are stochastic, they do not have access to perfect information about the images and instead extract only what is necessary to make predictions, making the agent robust to unseen images. From each state, a decoder reconstructs the corresponding image to learn general representations. Moreover, a small reward network is trained to rank outcomes during planning. To enable planning without generating images, a predictor learns to guess the stochastic representations without access to the images from which they were computed.

Learning process of the world model used by DreamerV2. The world model maintains recurrent states (h1–h3) that receive actions (a1–a2) and incorporate information about the images (x1–x3) via stochastic representations (z1–z3). A predictor guesses the representations as (ẑ1–ẑ3) without access to the images from which they were generated.

Importantly, DreamerV2 introduces two new techniques to RSSM that lead to a substantially more accurate world model for learning successful policies. The first technique is to represent each image with multiple categorical variables instead of the Gaussian variables used by PlaNet, DreamerV1, and many more world models in the literature [1, 2, 3, 4, 5]. This leads the world model to reason about the world in terms of discrete concepts and enables more accurate predictions of future representations.

The encoder turns each image into 32 distributions over 32 classes each, the meanings of which are determined automatically as the world model learns. The one-hot vectors sampled from these distributions are concatenated to a sparse representation that is passed on to the recurrent state. To backpropagate through the samples, we use straight-through gradients that are easy to implement using automatic differentiation. Representing images with categorical variables allows the predictor to accurately learn the distribution over the one-hot vectors of the possible next images. In contrast, earlier world models that use Gaussian predictors cannot accurately match the distribution over multiple Gaussian representations for the possible next images.

Multiple categoricals that represent possible next images can be accurately predicted by a categorical predictor, whereas a Gaussian predictor is not flexible enough to accurately predict multiple possible Gaussian representations.

The second new technique of DreamerV2 is KL balancing. Many previous world models use the ELBO objective that encourages accurate reconstructions while keeping the stochastic representations (posteriors) close to their predictions (priors) to regularize the amount of information extracted from each image and facilitate generalization. Because the objective is optimized end-to-end, the stochastic representations and their predictions can be made more similar by bringing either of the two towards the other. However, bringing the representations towards their predictions can be problematic when the predictor is not yet accurate. KL balancing lets the predictions move faster toward the representations than vice versa. This results in more accurate predictions, a key to successful planning.

Long-term video predictions of the world model for holdout sequences. Each model receives 5 frames as input (not shown) and then predicts 45 steps forward given only actions. The video predictions are only used to gain insights into the quality of the world model. During planning, only compact representations are predicted, not images.

Measuring Atari Performance
DreamerV2 is the first world model that enables learning successful behaviors with human-level performance on the well-established and competitive Atari benchmark. We select the 55 games that many previous studies have in common and recommend this set of games for future work. Following the standard evaluation protocol, the agents are allowed 200M environment interactions using an action repeat of 4 and sticky actions (25% chance that an action is ignored and the previous action is repeated instead). We compare to the top model-free agents IQN and Rainbow, as well as to the well-known C51 and DQN agents implemented in the Dopamine framework.

Different standards exist for aggregating the scores across the 55 games. Ideally, a new algorithm would perform better under all conditions. For all four aggregation methods, DreamerV2 indeed outperforms all compared model-free algorithms while using the same computational budget.

DreamerV2 outperforms the top model-free agents according to four methods for aggregating scores across the 55 Atari games. We introduce and recommend the Clipped Record Mean (right-most plot) as an informative and robust performance metric.

The first three aggregation methods were previously proposed in the literature. We identify important drawbacks in each and recommend a new aggregation method, the clipped record mean to overcome their drawbacks.

  • Gamer Median. Most commonly, scores for each game are normalized by the performance of a human gamer that was assessed for the DQN paper and the median of the normalized scores of all games is reported. Unfortunately, the median ignores the scores of many simpler and harder games.
  • Gamer Mean. The mean takes the scores for all games into account but is mainly influenced by a small number of games where the human gamer performed poorly. This makes it easy for an algorithm to achieve large normalized scores on some games (e.g., James Bond, Video Pinball) that then dominate the mean.
  • Record Mean. Prior work recommends normalization based on the human world record instead, but such a metric is still overly influenced by a small number of games where it is easy for the artificial agents to outscore the human record.
  • Clipped Record Mean. We introduce a new metric that normalizes scores by the world record and clips them to not exceed the record. This yields an informative and robust metric that takes the performance on all games into account to an approximately equal amount.

While many current algorithms exceed the human gamer baseline, they are still quite far behind the human world record. As shown in the right-most plot above, DreamerV2 leads by achieving 25% of the human record on average across games. Clipping the scores at the record line lets us focus our efforts on developing methods that come closer to the human world record on all of the games rather than exceeding it on just a few games.

What matters and what doesn't
To gain insights into the important components of DreamerV2, we conduct an extensive ablation study. Importantly, we find that categorical representations offer a clear advantage over Gaussian representations despite the fact that Gaussians have been used extensively in prior works. KL balancing provides an even more substantial advantage over the KL regularizer used by most generative models.

By preventing the image reconstruction or reward prediction gradients from shaping the model states, we study their importance for learning successful representations. We find that DreamerV2 relies completely on universal information from the high-dimensional input images and its representations enable accurate reward predictions even when they were not trained using information about the reward. This mirrors the success of unsupervised representation learning in the computer vision community.

Atari performance for various ablations of DreamerV2 (Clipped Record Mean). Categorical representations, KL balancing, and learning about the images are crucial for the success of DreamerV2. Using reward information, that is specific to narrow tasks, offers no additional benefits for learning the world model.

Conclusion
We show how to learn a powerful world model to achieve human-level performance on the competitive Atari benchmark and outperform the top model-free agents. This result demonstrates that world models are a powerful approach for achieving high performance on reinforcement learning problems and are ready to use for practitioners and researchers. We see this as an indication that the success of unsupervised representation learning in computer vision [1, 2] is now starting to be realized in reinforcement learning in the form of world models. An unofficial implementation of DreamerV2 is available on Github and provides a productive starting point for future research projects. We see world models that leverage large offline datasets, long-term memory, hierarchical planning, and directed exploration as exciting avenues for future research.

Acknowledgements
This project is a collaboration with Timothy Lillicrap, Mohammad Norouzi, and Jimmy Ba. We further thank everybody on the Brain Team and beyond who commented on our paper draft and provided feedback at any point throughout the project.

Source: Google AI Blog


A Simulation Suite for Tackling Applied Reinforcement Learning Challenges

Posted by Daniel J. Mankowitz, Research Scientist, DeepMind and Gabriel Dulac-Arnold, Research Scientist, Google Research

Reinforcement Learning (RL) has proven to be effective in solving numerous complex problems ranging from Go, StarCraft and Minecraft to robot locomotion and chip design. In each of these cases, a simulator is available or the real environment is quick and inexpensive to access. Yet, there are still considerable challenges to deploying RL to real-world products and systems. For example, in physical control systems, such as robotics and autonomous driving, RL controllers are trained to solve tasks like grasping objects or driving on a highway. These controllers are susceptible to effects such as sensor noise, system delays, or normal wear-and-tear that can reduce the quality of input to the controller, leading to incorrect decision-making and potentially catastrophic failures.

A physical control system: Robots learning how to grasp and sort objects using RL at the Everyday Robot Project at X. These types of systems are subject to many of the real-world challenges detailed here.

In “Challenges of Real-World Reinforcement Learning”, we identify and discuss nine different challenges that hinder the application of current RL algorithms to applied systems. We then follow up this work with an empirical investigation in which we simulated versions of these challenges on state-of-the-art RL algorithms, and benchmark the effects of each. We have open-sourced these simulated challenges in the Real-World RL (RWRL) task suite to help draw attention to these important issues, as well as accelerate research toward solving them.

The RWRL Suite
The RWRL suite is a set of simulated tasks inspired by applied reinforcement learning challenges, the goal of which is to enable fast algorithmic iterations for both researchers and practitioners, without having to run slow, expensive experiments on real-systems. While there will be additional challenges transitioning from RL algorithms that were trained in simulation to real-world applications, this suite intends to close some of the more fundamental, algorithmic gaps. At present, RWRL supports a subset of the DeepMind Control Suite domains, but the goal is to broaden the suite to support an even more diverse domain set.

Easy-to-Use & Flexible
We designed the suite with two main goals in mind. (1) It should be easy to use — a user should be able to start running experiments within minutes of downloading the suite, simply by changing a few lines of code. (2) It should be flexible — a user should be able to incorporate any combination of challenges into the environment with very little effort.

A Delayed Action Example
To illustrate the ease of use of the RWRL suite, imagine a researcher or practitioner wants to implement action delays (i.e., temporal delays on actions being sent to the environment). To use the RWRL suite, simply import the rwrl module. Next, load an environment (e.g., cartpole) with the delay_spec argument. This optional argument is specified as a dictionary configuring delay applied to actions, observations, or rewards and the number of timesteps the corresponding element is delayed (e.g., 20 timesteps). Once the environment is loaded, the effects of actions are automatically delayed without any other changes to the experiment. This makes it easy to test an RL algorithm with action delays in a range of different environments supported by the RWRL suite.

A high-level overview of the RWRL suite. Add a challenge (e.g., action delays) into the environment with a few lines of code, run a hyperparameter sweep and produce a graph shown on the right

A user can combine different challenges or choose from a set of predefined benchmark challenges by simply adding additional arguments to the load function, all of which are specified in the open-source RWRL suite codebase.

Supported Challenges
The RWRL suite provides functionality to support experiments related to eight of the nine different challenges that make applying current RL algorithms on applied systems difficult: sample efficiency; system delays; high-dimensional state and action spaces; constraints; partial observability, stochasticity and non-stationarity; multiple objectives; real-time inference; and training from offline logs. RWRL excludes the explainability challenge, which is abstract and non-trivial to define. The supported experiments are non-exhaustive and provide researchers and practitioners with the ability to analyze the capabilities of their agent with respect to each challenge dimension. Examples of the supported challenges include:

  • System Delays
    Most real systems have delays in either sensing, actuation or reward feedback, all of which can be configured and applied to any task within the RWRL suite.The graphs below show the performance of a D4PG agent as actions (left), observations (middle) and rewards (right) are increasingly delayed.

    The effect of increasing the action (left), observation (middle) and reward (right) delays respectively on a state-of-the art RL agent in four MuJoCo domains.

    As can be seen in the graphs, a researcher or practitioner can quickly gain insights as to which type of delay affects their agent’s performance. These delays can also be combined together to observe their combined effect.

  • Constraints
    Almost all applied systems have some form of constraints embedded into the overall objective, which is not common in most RL environments. The RWRL suite implements a series of constraints for each task, with varying difficulties, to facilitate research in constrained RL. An example of a complex local angular velocity constraint being violated is visualized in the video below.
    An example of constraint violations for cartpole. The red screen indicates that a violation has occurred on localized angular velocity.
  • Non-Stationarity
    The user can introduce non-stationarity by perturbing environment parameters. These perturbations are in contrast to the pixel level adversarial perturbations that have recently gained popularity in research on supervised deep learning. For example, in the human walker domain, the size of the head and friction of the ground can be modified throughout training to simulate changing conditions. A variety of schedulers are available in the RWRL suite (see our codebase for more details), along with multiple default parameter perturbations, which were carefully defined to handicap the learning capabilities of state-of-the-art learning algorithms.
    Non-stationary perturbations. The suite supports perturbing environment parameters across episodes such as changing head size (center) and contact friction (right).
  • Training from Offline Log Data
    In most applied systems, it is both slow and expensive to run experiments. There are often logs of data available from previous experiments that can be utilized to train a policy. However, it is often difficult to outperform the previous model in production due to the data being limited, of low variance, or of poor quality. To address this, we have generated offline datasets of the combined RWRL benchmark challenges, which we made available as part of a wider offline dataset release. More information can be found in this notebook.

Conclusion
Most systems rarely manifest only a single challenge, and we are excited to see how algorithms can deal with an environment in which there are multiple challenges combined with increasing levels of difficulty (‘Easy’, ‘Medium’ and ‘Hard’). We highly encourage the research community to try and solve these challenges, as we believe that solving them will facilitate more widespread applications of RL to products and real-world systems.

While the initial set of RWRL suite features and experiments provide a starting point for closing the gap between the current state of RL and the challenges of applied systems, there is still much work to do. The supported experiments are not exhaustive and we welcome new ideas from the wider community to better evaluate the capabilities of our RL agents. Our main goal with this suite is to highlight and encourage research on the core problems that limit the effectiveness of RL algorithms in applied products and systems and to accelerate progress towards enabling future RL applications.

Acknowledgements
We would like to thank our core contributor and co-author Nir Levine for his invaluable help. We would also like to thank our co-authors Jerry Li, Sven Gowal, Todd Hester and Cosmin Paduraru as well as Robert Dadashi, the ACME team, Dan A. Calian, Juliet Rothenberg and Timothy Mann for their contributions.

Source: Google AI Blog


Introducing Dreamer: Scalable Reinforcement Learning Using World Models

Posted by Danijar Hafner, Student Researcher, Google Research

Research into how artificial agents can choose actions to achieve goals is making rapid progress in large part due to the use of reinforcement learning (RL). Model-free approaches to RL, which learn to predict successful actions through trial and error, have enabled DeepMind's DQN to play Atari games and AlphaStar to beat world champions at Starcraft II, but require large amounts of environment interaction, limiting their usefulness for real-world scenarios.

In contrast, model-based RL approaches additionally learn a simplified model of the environment. This world model lets the agent predict the outcomes of potential action sequences, allowing it to play through hypothetical scenarios to make informed decisions in new situations, thus reducing the trial and error necessary to achieve goals. In the past, it has been challenging to learn accurate world models and leverage them to learn successful behaviors. While recent research, such as our Deep Planning Network (PlaNet), has pushed these boundaries by learning accurate world models from images, model-based approaches have still been held back by ineffective or computationally expensive planning mechanisms, limiting their ability to solve difficult tasks.

Today, in collaboration with DeepMind, we present Dreamer, an RL agent that learns a world model from images and uses it to learn long-sighted behaviors. Dreamer leverages its world model to efficiently learn behaviors via backpropagation through model predictions. By learning to compute compact model states from raw images, the agent is able to efficiently learn from thousands of predicted sequences in parallel using just one GPU. Dreamer achieves a new state-of-the-art in performance, data efficiency and computation time on a benchmark of 20 continuous control tasks given raw image inputs. To stimulate further advancement of RL, we are releasing the source code to the research community.

How Does Dreamer Work?
Dreamer consists of three processes that are typical for model-based methods: learning the world model, learning behaviors from predictions made by the world model, and executing its learned behaviors in the environment to collect new experience. To learn behaviors, Dreamer uses a value network to take into account rewards beyond the planning horizon and an actor network to efficiently compute actions. The three processes, which can be executed in parallel, are repeated until the agent has achieved its goals:
The three processes of the Dreamer agent. The world model is learned from past experience. From predictions of this model, the agent then learns a value network to predict future rewards and an actor network to select actions. The actor network is used to interact with the environment.
Learning the World Model
Dreamer leverages the PlaNet world model, which predicts outcomes based on a sequence of compact model states that are computed from the input images, instead of directly predicting from one image to the next. It automatically learns to produce model states that represent concepts helpful for predicting future outcomes, such as object types, positions of objects, and the interaction of the objects with their surroundings. Given a sequence of images, actions, and rewards from the agent's dataset of past experience, Dreamer learns the world model as shown:
Dreamer learns a world model from experience. Using past images (o1–o3) and actions (a1–a2), it computes a sequence of compact model states (green circles) from which it reconstructs the images (ô1–ô3) and predicts the rewards (r̂1–r̂3).
An advantage to using the PlaNet world model is that predicting ahead using compact model states instead of images greatly improves the computational efficiency. This enables the model to predict thousands of sequences in parallel on a single GPU. The approach can also facilitate generalization, leading to accurate long-term video predictions. To gain insights into how the model works, we can visualize the predicted sequences by decoding the compact model states back into images, as shown below for a task of the DeepMind Control Suite and for a task of the DeepMind Lab environment:
Predicting ahead using compact model states enables long-term predictions in complex environments. Shown here are two sequences that the agent has not encountered before. Given five input images, the model reconstructs them and predicts the future images up to time step 50.
Efficient Behavior Learning
Previously developed model-based agents typically select actions either by planning through many model predictions or by using the world model in place of a simulator to reuse existing model-free techniques. Both designs are computationally demanding and do not fully leverage the learned world model. Moreover, even powerful world models are limited in how far ahead they can accurately predict, rendering many previous model-based agents shortsighted. Dreamer overcomes these limitations by learning a value network and an actor network via backpropagation through predictions of its world model.

Dreamer efficiently learns the actor network to predict successful actions by propagating gradients of rewards backwards through predicted state sequences, which is not possible for model-free approaches. This tells Dreamer how small changes to its actions affect what rewards are predicted in the future, allowing it to refine the actor network in the direction that increases the rewards the most. To consider rewards beyond the prediction horizon, the value network estimates the sum of future rewards for each model state. The rewards and values are then backpropagated to refine the actor network to select improved actions:
Dreamer learns long-sighted behaviors from predicted sequences of model states. It first learns the long-term value (v̂2–v̂3) of each state, and then predicts actions (â1–â2) that lead to high rewards and values by backpropagating them through the state sequence to the actor network.
Dreamer differs from PlaNet in several ways. For a given situation in the environment, PlaNet searches for the best action among many predictions for different action sequences. In contrast, Dreamer side-steps this expensive search by decoupling planning and acting. Once its actor network has been trained on predicted sequences, it computes the actions for interacting with the environment without additional search. In addition, Dreamer considers rewards beyond the planning horizon using a value function and leverages backpropagation for efficient planning.

Performance on Control Tasks
We evaluated Dreamer on a standard benchmark of 20 diverse tasks with continuous actions and image inputs. The tasks include balancing and catching objects, as well as locomotion of various simulated robots. The tasks are designed to pose a variety of challenges to the RL agent, including difficult to predict collisions, sparse rewards, chaotic dynamics, small but relevant objects, high degrees of freedom, and 3D perspectives:
Dreamer learns to solve 20 challenging continuous control tasks with image inputs, 5 of which are displayed here. The visualizations show the same 64x64 images that the agent receives from the environment.
We compare the performance of Dreamer to that of PlaNet, the previous best model-based agent, the popular model-free agent, A3C, as well as the current best model-free agent on this benchmark, D4PG, which combines several advances of model-free RL. The model-based agents learn efficiently in under 5 million frames, corresponding to 28 hours inside the simulation. The model-free agents learn more slowly and require 100 million frames, corresponding to 23 days inside the simulation.

On the benchmark of 20 tasks, Dreamer outperforms the best model-free agent (D4PG) with an average score of 823 compared to 786, while learning from 20 times fewer environment interactions. Moreover, it exceeds the final performance of the previously best model-based agent (PlaNet) across almost all of the tasks. The computation time of 16 hours for training Dreamer is less than the 24 hours required for the other methods. The final performance of the four agents is shown below:
Dreamer outperforms the previous best model-free (D4PG) and model-based (PlaNet) methods on the benchmark of 20 tasks in terms of final performance, data efficiency, and computation time.
In addition to our main experiments on continuous control tasks, we demonstrate the generality of Dreamer by applying it to tasks with discrete actions. For this, we select Atari games and DeepMind Lab levels that require both reactive and long-sighted behavior, spatial awareness, and understanding of visually more diverse scenes. The resulting behaviors are visualized below, showing that Dreamer also efficiently learns to solve these more challenging tasks:
Dreamer learns successful behaviors on Atari games and DeepMind Lab levels, which feature discrete actions and visually more diverse scenes, including 3D environments with multiple objects.
Conclusion
Our work demonstrates that learning behaviors from sequences predicted by world models alone can solve challenging visual control tasks from image inputs, surpassing the performance of previous model-free approaches. Moreover, Dreamer demonstrates that learning behaviors by backpropagating value gradients through predicted sequences of compact model states is successful and robust, solving a diverse collection of continuous and discrete control tasks. We believe that Dreamer offers a strong foundation for further pushing the limits of reinforcement learning, including better representation learning, directed exploration with uncertainty estimates, temporal abstraction, and multi-task learning.

Acknowledgements
This project is a collaboration with Timothy Lillicrap, Jimmy Ba, and Mohammad Norouzi. We further thank everybody in the Brain Team and beyond who commented on our paper draft and provided feedback at any point throughout the project.

Source: Google AI Blog


Introducing PlaNet: A Deep Planning Network for Reinforcement Learning

Posted by Danijar Hafner, Student Researcher, Google AI

Research into how artificial agents can improve their decisions over time is progressing rapidly via reinforcement learning (RL). For this technique, an agent observes a stream of sensory inputs (e.g. camera images) while choosing actions (e.g. motor commands), and sometimes receives a reward for achieving a specified goal. Model-free approaches to RL aim to directly predict good actions from the sensory observations, enabling DeepMind's DQN to play Atari and other agents to control robots. However, this blackbox approach often requires several weeks of simulated interaction to learn through trial and error, limiting its usefulness in practice.

Model-based RL, in contrast, attempts to have agents learn how the world behaves in general. Instead of directly mapping observations to actions, this allows an agent to explicitly plan ahead, to more carefully select actions by "imagining" their long-term outcomes. Model-based approaches have achieved substantial successes, including AlphaGo, which imagines taking sequences of moves on a fictitious board with the known rules of the game. However, to leverage planning in unknown environments (such as controlling a robot given only pixels as input), the agent must learn the rules or dynamics from experience. Because such dynamics models in principle allow for higher efficiency and natural multi-task learning, creating models that are accurate enough for successful planning is a long-standing goal of RL.

To spur progress on this research challenge and in collaboration with DeepMind, we present the Deep Planning Network (PlaNet) agent, which learns a world model from image inputs only and successfully leverages it for planning. PlaNet solves a variety of image-based control tasks, competing with advanced model-free agents in terms of final performance while being 5000% more data efficient on average. We are additionally releasing the source code for the research community to build upon.
The PlaNet agent learning to solve a variety of continuous control tasks from images in 2000 attempts. Previous agents that do not learn a model of the environment often require 50 times as many attempts to reach comparable performance.
How PlaNet Works
In short, PlaNet learns a dynamics model given image inputs and efficiently plans with it to gather new experience. In contrast to previous methods that plan over images, we rely on a compact sequence of hidden or latent states. This is called a latent dynamics model: instead of directly predicting from one image to the next image, we predict the latent state forward. The image and reward at each step is then generated from the corresponding latent state. By compressing the images in this way, the agent can automatically learn more abstract representations, such as positions and velocities of objects, making it easier to predict forward without having to generate images along the way.
Learned Latent Dynamics Model: In a latent dynamics model, the information of the input images is integrated into the hidden states (green) using the encoder network (grey trapezoids). The hidden state is then projected forward in time to predict future images (blue trapezoids) and rewards (blue rectangle).
To learn an accurate latent dynamics model, we introduce:
  • A Recurrent State Space Model: A latent dynamics model with both deterministic and stochastic components, allowing to predict a variety of possible futures as needed for robust planning, while remembering information over many time steps. Our experiments indicate both components to be crucial for high planning performance.
  • A Latent Overshooting Objective: We generalize the standard training objective for latent dynamics models to train multi-step predictions, by enforcing consistency between one-step and multi-step predictions in latent space. This yields a fast and effective objective that improves long-term predictions and is compatible with any latent sequence model.
While predicting future images allows us teach the model, encoding and decoding images (trapezoids in the figure above) requires significant computation, which would slow down planning. However, planning in the compact latent state space is fast since we only need to predict future rewards, and not images, to evaluate an action sequence. For example, the agent can imagine how the position of a ball and its distance to the goal will change for certain actions, without having to visualize the scenario. This allows us to compare 10,000 imagined action sequences with a large batch size every time the agent chooses an action. We then execute the first action of the best sequence found and replan at the next step.
Planning in Latent Space: For planning, we encode past images (gray trapezoid) into the current hidden state (green). From there, we efficiently predict future rewards for multiple action sequences. Note how the expensive image decoder (blue trapezoid) from the previous figure is gone. We then execute the first action of the best sequence found (red box).
Compared to our preceding work on world models, PlaNet works without a policy network -- it chooses actions purely by planning, so it benefits from model improvements on the spot. For the technical details, check out our online research paper or the PDF version.

PlaNet vs. Model-Free Methods
We evaluate PlaNet on continuous control tasks. The agent is only given image observations and rewards. We consider tasks that pose a variety of different challenges:
  • A cartpole swing-up task, with a fixed camera, so the cart can move out of sight. The agent thus must absorb and remember information over multiple frames.
  • A finger spin task that requires predicting two separate objects, as well as the interactions between them.
  • A cheetah running task that includes contacts with the ground that are difficult to predict precisely, calling for a model that can predict multiple possible futures.
  • A cup task, which only provides a sparse reward signal once a ball is caught. This demands accurate predictions far into the future to plan a precise sequence of actions.
  • A walker task, in which a simulated robot starts off by lying on the ground, and must first learn to stand up and then walk.
PlaNet agents trained on a variety of image-based control tasks. The animation shows the input images as the agent is solving the tasks. The tasks pose different challenges: partial observability, contacts with the ground, sparse rewards for catching a ball, and controlling a challenging bipedal robot.
Our work constitutes one of the first examples where planning with a learned model outperforms model-free methods on image-based tasks. The table below compares PlaNet to the well-known A3C agent and the D4PG agent, that combines recent advances in model-free RL. The numbers for these baselines are taken from the DeepMind Control Suite. PlaNet clearly outperforms A3C on all tasks and reaches final performance close to D4PG while, using 5000% less interaction with the environment on average.
One Agent for All Tasks
Additionally, we train a single PlaNet agent to solve all six tasks. The agent is randomly placed into different environments without knowing the task, so it needs to infer the task from its image observations. Without changes to the hyper parameters, the multi-task agent achieves the same mean performance as individual agents. While learning slower on the cartpole tasks, it learns substantially faster and reaches a higher final performance on the challenging walker task that requires exploration.
Video predictions of the PlaNet agent trained on multiple tasks. Holdout episodes collected with the trained agent are shown above and open-loop agent hallucinations below. The agent observes the first 5 frames as context to infer the task and state and accurately predicts ahead for 50 steps given a sequence of actions.
Conclusion
Our results showcase the promise of learning dynamics models for building autonomous RL agents. We advocate for further research that focuses on learning accurate dynamics models on tasks of even higher difficulty, such as 3D environments and real-world robotics tasks. A possible ingredient for scaling up is the processing power of TPUs. We are excited about the possibilities that model-based reinforcement learning opens up, including multi-task learning, hierarchical planning and active exploration using uncertainty estimates.

Acknowledgements
This project is a collaboration with Timothy Lillicrap, Ian Fischer, Ruben Villegas, Honglak Lee, David Ha and James Davidson. We further thank everybody who commented on our paper draft and provided feedback at any point throughout the project.




Source: Google AI Blog


Curiosity and Procrastination in Reinforcement Learning

Posted by Nikolay Savinov, Research Intern, Google Brain Team and Timothy Lillicrap, Research Scientist, DeepMind

Reinforcement learning (RL) is one of the most actively pursued research techniques of machine learning, in which an artificial agent receives a positive reward when it does something right, and negative reward otherwise. This carrot-and-stick approach is simple and universal, and allowed DeepMind to teach the DQN algorithm to play vintage Atari games and AlphaGoZero to play the ancient game of Go. This is also how OpenAI taught its OpenAI-Five algorithm to play the modern video game Dota, and how Google taught robotic arms to grasp new objects. However, despite the successes of RL, there are many challenges to making it an effective technique.

Standard RL algorithms struggle with environments where feedback to the agent is sparse — crucially, such environments are common in the real world. As an example, imagine trying to learn how to find your favorite cheese in a large maze-like supermarket. You search and search but the cheese section is nowhere to be found. If at every step you receive no “carrot” and no “stick”, there’s no way to tell if you are headed in the right direction or not. In the absence of rewards, what is to stop you from wandering around in circles? Nothing, except perhaps your curiosity, which motivates you go into a product section that looks unfamiliar to you in pursuit of your sought-after cheese.

In “Episodic Curiosity through Reachability” — the result of a collaboration between the Google Brain team, DeepMind and ETH Zürich — we propose a novel episodic memory-based model of granting RL rewards, akin to curiosity, which leads to exploring the environment. Since we want the agent not only to explore the environment but also to solve the original task, we add a reward bonus provided by our model to the original sparse task reward. The combined reward is not sparse anymore which allows standard RL algorithms to learn from it. Thus, our curiosity method expands the set of tasks which are solvable with RL.
Episodic Curiosity through Reachability: Observations are added to memory, reward is computed based on how far the current observation is from the most similar observation in memory. The agent receives more reward for seeing observations which are not yet represented in memory.
The key idea of our method is to store the agent's observations of the environment in an episodic memory, while also rewarding the agent for reaching observations not yet represented in memory. Being “not in memory” is the definition of novelty in our method — seeking such observations means seeking the unfamiliar. Such a drive to seek the unfamiliar will lead the artificial agent to new locations, thus keeping it from wandering in circles and ultimately help it stumble on the goal. As we will discuss later, our formulation can save the agent from undesired behaviours which some other formulations are prone to. Much to our surprise, those behaviours bear some similarity to what a layperson would call “procrastination”.

Previous Curiosity Formulations
While there have been many attempts to formulate curiosity in the past[1][2][3][4], in this post we  focus on one natural and very popular approach: curiosity through prediction-based surprise, explored in the recent paper “Curiosity-driven Exploration by Self-supervised Prediction” (commonly referred to as the ICM method). To illustrate how surprise leads to curiosity, again consider our analogy of looking for cheese in a supermarket.
Illustration © Indira Pasko, used under CC BY-NC-ND 4.0 license.
As you wander throughout the market, you try to predict the future (“Now I’m in the meat section, so I think the section around the corner is the fish section — those are usually adjacent in this supermarket chain”). If your prediction is wrong, you are surprised (“No, it’s actually the vegetables section. I didn’t expect that!”) and thus rewarded. This makes you more motivated to look around the corner in the future, exploring new locations just to see if your expectations about them meet the reality (and, hopefully, stumble upon the cheese).

Similarly, the ICM method builds a predictive model of the dynamics of the world and gives the agent rewards when the model fails to make good predictions — a marker of surprise or novelty. Note that exploring unvisited locations is not directly a part of the ICM curiosity formulation. For the ICM method, visiting them is only a way to obtain more “surprise” and thus maximize overall rewards. As it turns out, in some environments there could be other ways to inflict self-surprise, leading to unforeseen results.
Agent imbued with surprise-based curiosity gets stuck when it encounters TV. GIF adopted from a video by © Deepak Pathak, used under CC BY 2.0 license.
The Dangers of “Procrastination”
In "Large-Scale Study of Curiosity-Driven Learning", the authors of the ICM method along with researchers from OpenAI show a hidden danger of surprise maximization: agents can learn to indulge procrastination-like behaviour instead of doing something useful for the task at hand. To see why, consider a common thought experiment the authors call the “noisy TV problem”, in which an agent is put into a maze and tasked with finding a highly rewarding item (akin to “cheese” in our previous supermarket example). The environment also contains a TV for which the agent has the remote control. There is a limited number of channels (each with a distinct show) and every press on the remote control switches to a random channel. How would an agent perform in such an environment?

For the surprise-based curiosity formulation, changing channels would result in a large reward, as each change is unpredictable and surprising. Crucially, even after cycling through all the available channels, the random channel selection ensures every new change will still be surprising — the agent is making predictions about what will be on the TV after a channel change, and will very likely be wrong, leading to surprise. Importantly, even if the agent has already seen every show on every channel, the change is still unpredictable. Because of this, the agent imbued with surprise-based curiosity would eventually stay in front of the TV forever instead of searching for a highly rewarding item — akin to procrastination. So, what would be a definition of curiosity which does not lead to such behaviour?

Episodic Curiosity
In “Episodic Curiosity through Reachability”, we explore an episodic memory-based curiosity model that turns out to be less prone to “self-indulging” instant gratification. Why so? Using our example above, after changing channels for a while, all of the shows will end up in memory. Thus, the TV won’t be so attractive anymore: even if the order of shows appearing on the screen is random and unpredictable, all those shows are already in memory! This is the main difference to the surprise-based methods: our method doesn’t even try to make bets about the future which could be hard (or even impossible) to predict. Instead, the agent examines the past to know if it has seen observations similar to the current one. Thus our agent won’t be drawn that much to the instant gratification provided by the noisy TV. It will have to go and explore the world outside of the TV to get more reward.

But how do we decide whether the agent is seeing the same thing as an existing memory? Checking for an exact match could be meaningless: in a realistic environment, the agent rarely sees exactly the same thing twice. For example, even if the agent returned to exactly the same room, it would still see this room under a different angle compared to its memories.

Instead of checking for an exact match in memory, we use a deep neural network that is trained to measure how similar two experiences are. To train this network, we have it guess whether two observations were experienced close together in time, or far apart in time. Temporal proximity is a good proxy for whether two experiences should be judged to be part of the same experience. This training leads to a general concept of novelty via reachability which is illustrated below.
Graph of reachabilities would determine novelty. In practice, this graph is not available — so we train a neural network approximator to estimate a number of steps between observations.
Experimental Results
To compare the performance of different approaches to curiosity, we tested them in two visually rich 3D environments: ViZDoom and DMLab. In those environments, the agent was tasked with various problems like searching for a goal in a maze or collecting good and avoiding bad objects. The DMLab environment happens to provide the agent with a laser-like science fiction gadget. The standard setting in the previous work on DMLab was to equip the agent with this gadget for all tasks, and if the agent does not need a gadget for a particular task, it is free not to use it. Interestingly, similar to the noisy TV experiment described above, the surprise-based ICM method actually uses this gadget a lot even when it is useless for the task at hand! When tasked with searching for a high-rewarding item in the maze, it instead prefers to spend time tagging walls because this yields a lot of “surprise” reward. Theoretically, predicting the result of tagging should be possible, but in practice is too hard as it apparently requires a deeper knowledge of physics than is available to a standard agent.
Surprise-based ICM method is persistently tagging the wall instead of exploring the maze.
Our method instead learns reasonable exploration behaviour under the same conditions. This is because it does not try to predict the result of its actions, but rather seeks observations which are “harder” to achieve from those already in the episodic memory. In other words, the agent implicitly pursues goals which require more effort to reach from memory than just a single tagging action.
Our method shows reasonable exploration.
It is interesting to see that our approach to granting reward penalizes an agent running in circles. This is because after completing the first circle the agent does not encounter new observations other than those in memory, and thus receives no reward:
Our reward visualization: red means negative reward, green means positive reward. Left to right: map with rewards, map with locations currently in memory, first-person view.
At the same time, our method favors good exploration behavior:
Our reward visualization: red means negative reward, green means positive reward. Left to right: map with rewards, map with locations currently in memory, first-person view.
We hope that our work will help lead to a new wave of exploration methods, going beyond surprise and learning more intelligent exploration behaviours. For an in-depth analysis of our method, please take a look at the preprint of our research paper.

Acknowledgements:
This project is a result of a collaboration between the Google Brain team, DeepMind and ETH Zürich. The core team includes Nikolay Savinov, Anton Raichuk, Raphaël Marinier, Damien Vincent, Marc Pollefeys, Timothy Lillicrap and Sylvain Gelly. We would like to thank Olivier Pietquin, Carlos Riquelme, Charles Blundell and Sergey Levine for the discussions about the paper. We are grateful to Indira Pasko for the help with illustrations.

References:
[1] "Count-Based Exploration with Neural Density Models", Georg Ostrovski, Marc G. Bellemare, Aaron van den Oord, Remi Munos
[2] "#Exploration: A Study of Count-Based Exploration for Deep Reinforcement Learning", Haoran Tang, Rein Houthooft, Davis Foote, Adam Stooke, Xi Chen, Yan Duan, John Schulman, Filip De Turck, Pieter Abbeel
[3] "Unsupervised Learning of Goal Spaces for Intrinsically Motivated Goal Exploration", Alexandre Péré, Sébastien Forestier, Olivier Sigaud, Pierre-Yves Oudeyer
[4] "VIME: Variational Information Maximizing Exploration", Rein Houthooft, Xi Chen, Yan Duan, John Schulman, Filip De Turck, Pieter Abbeel

Source: Google AI Blog


Open-sourcing DeepMind Lab

Originally posted on DeepMind Blog

DeepMind's scientific mission is to push the boundaries of AI, developing systems that can learn to solve any complex problem without needing to be taught how. To achieve this, we work from the premise that AI needs to be general. Agents should operate across a wide range of tasks and be able to automatically adapt to changing circumstances. That is, they should not be pre-programmed, but rather, able to learn automatically from their raw inputs and reward signals from the environment. There are two parts to this research program: (1)  designing ever-more intelligent agents capable of more-and-more sophisticated cognitive skills, and (2) building increasingly complex environments where agents can be trained and evaluated.

The development of innovative agents goes hand in hand with the careful design and implementation of rationally selected, flexible and well-maintained environments. To that end, we at DeepMind have invested considerable effort toward building rich simulated environments to serve as  “laboratories” for AI research. Now we are open-sourcing our flagship platform,  DeepMind Lab, so the broader research community can make use of it.

DeepMind Lab is a fully 3D game-like platform tailored for agent-based AI research. It is observed from a first-person viewpoint, through the eyes of the simulated agent. Scenes are rendered with rich science fiction-style visuals. The available actions allow agents to look around and move in 3D. The agent’s “body” is a floating orb. It levitates and moves by activating thrusters opposite its desired direction of movement, and it has a camera that moves around the main sphere as a ball-in-socket joint tracking the rotational look actions. Example tasks include collecting fruit, navigating in mazes, traversing dangerous passages while avoiding falling off cliffs, bouncing through space using launch pads to move between platforms, playing laser tag, and quickly learning and remembering random procedurally generated environments. An illustration of how agents in DeepMind Lab perceive and interact with the world can be seen below:

At each moment in time, agents observe the world as an image, in pixels, rendered from their own first-person perspective. They also may receive a reward (or punishment!) signal. The agent can activate its thrusters to move in 3D and can also rotate its viewpoint along both horizontal and vertical axes.


Artificial general intelligence research in DeepMind Lab emphasizes navigation, memory, 3D vision from a first person viewpoint, motor control, planning, strategy, time, and fully autonomous agents that must learn for themselves what tasks to perform by exploring their environment. All these factors make learning difficult. Each are considered frontier research questions in their own right. Putting them all together in one platform, as we have, represents a significant new challenge for the field.


DeepMind Lab is highly customisable and extendable. New levels can be authored with off-the-shelf editor tools. In addition, DeepMind Lab includes an interface for programmatic level-creation. Levels can be customised with gameplay logic, item pickups, custom observations, level restarts, reward schemes, in-game messages and more. The interface can be used to create levels in which novel map layouts are generated on the fly while an agent trains. These features are useful in, for example, testing how an agent copes with unfamiliar environments. Users will be able to add custom levels to the platform via GitHub. The assets will be hosted on GitHub alongside all the code, maps and level scripts. Our hope is that the community will help us shape and develop the platform going forward.



DeepMind Lab has been used internally at DeepMind for some time (example). We believe it has already had a significant impact on our thinking concerning numerous aspects of intelligence, both natural and artificial. However, our efforts so far have only barely scratched the surface of what is possible in DeepMind Lab. There are opportunities for significant contributions still to be made in a number of mostly still untouched research domains now available through DeepMind Lab, such as navigation, memory and exploration.

As well as facilitating agent evaluation, there are compelling reasons to think that it may be fundamentally easier to develop intelligence in a 3D world, observed from a first-person viewpoint, like DeepMind Lab. After all, the only known examples of general-purpose intelligence in the natural world arose from a combination of evolution, development, and learning, grounded in physics and the sensory apparatus of animals. It is possible that a large fraction of animal and human intelligence is a direct consequence of the richness of our environment, and unlikely to arise without it. Consider the alternative: if you or I had grown up in a world that looked like Space Invaders or Pac-Man, it doesn’t seem likely we would have achieved much general intelligence!

Read the full paper here.

Access DeepMind's GitHub repository here.

By Charlie Beattie, Joel Leibo, Stig Petersen and Shane Legg, DeepMind Team


How Robots Can Acquire New Skills from Their Shared Experience

Posted by Sergey Levine (Google Brain Team), Timothy Lillicrap (DeepMind), Mrinal Kalakrishnan (X)

The ability to learn from experience will likely be a key in enabling robots to help with complex real-world tasks, from assisting the elderly with chores and daily activities, to helping us in offices and hospitals, to performing jobs that are too dangerous or unpleasant for people. However, if each robot must learn its full repertoire of skills for these tasks only from its own experience, it could take far too long to acquire a rich enough range of behaviors to be useful. Could we bridge this gap by making it possible for robots to collectively learn from each other’s experiences?

While machine learning algorithms have made great strides in natural language understanding and speech recognition, the kind of symbolic high-level reasoning that allows people to communicate complex concepts in words remains out of reach for machines. However, robots can instantaneously transmit their experience to other robots over the network - sometimes known as "cloud robotics" - and it is this ability that can let them learn from each other.

This is true even for seemingly simple low-level skills. Humans and animals excel at adaptive motor control that integrates their senses, reflexes, and muscles in a closely coordinated feedback loop. Robots still struggle with these basic skills in the real world, where the variability and complexity of the environment demands well-honed behaviors that are not easily fooled by distractors. If we enable robots to transmit their experiences to each other, could they learn to perform motion skills in close coordination with sensing in realistic environments?

We previously wrote about how multiple robots could pool their experiences to learn a grasping task. Here, we will discuss new experiments that we conducted to investigate three possible approaches for general-purpose skill learning across multiple robots: learning motion skills directly from experience, learning internal models of physics, and learning skills with human assistance. In all three cases, multiple robots shared their experiences to build a common model of the skill. The skills learned by the robots are still relatively simple -- pushing objects and opening doors -- but by learning such skills more quickly and efficiently through collective learning, robots might in the future acquire richer behavioral repertoires that could eventually make it possible for them to assist us in our daily lives.

Learning from raw experience with model-free reinforcement learning.
Perhaps one of the simplest ways for robots to teach each other is to pool information about their successes and failures in the world. Humans and animals acquire many skills by direct trial-and-error learning. During this kind of ‘model-free’ learning -- so called because there is no explicit model of the environment formed -- they explore variations on their existing behavior and then reinforce and exploit the variations that give bigger rewards. In combination with deep neural networks, model-free algorithms have recently proved to be surprisingly effective and have been key to successes with the Atari video game system and playing Go. Having multiple robots allows us to experiment with sharing experiences to speed up this kind of direct learning in the real world.

In these experiments we tasked robots with trying to move their arms to goal locations, or reaching to and opening a door. Each robot has a copy of a neural network that allows it to estimate the value of taking a given action in a given state. By querying this network, the robot can quickly decide what actions might be worth taking in the world. When a robot acts, we add noise to the actions it selects, so the resulting behavior is sometimes a bit better than previously observed, and sometimes a bit worse. This allows each robot to explore different ways of approaching a task. Records of the actions taken by the robots, their behaviors, and the final outcomes are sent back to a central server. The server collects the experiences from all of the robots and uses them to iteratively improve the neural network that estimates value for different states and actions. The model-free algorithms we employed look across both good and bad experiences and distill these into a new network that is better at understanding how action and success are related. Then, at regular intervals, each robot takes a copy of the updated network from the server and begins to act using the information in its new network. Given that this updated network is a bit better at estimating the true value of actions in the world, the robots will produce better behavior. This cycle can then be repeated to continue improving on the task. In the video below, a robot explores the door opening task.
With a few hours of practice, robots sharing their raw experience learn to make reaches to targets, and to open a door by making contact with the handle and pulling. In the case of door opening, the robots learn to deal with the complex physics of the contacts between the hook and the door handle without building an explicit model of the world, as can be seen in the example below:
Learning how the world works by interacting with objects.
Direct trial-and-error reinforcement learning is a great way to learn individual skills. However, humans and animals don’t learn exclusively by trial and error. We also build mental models about our environment and imagine how the world might change in response to our actions.

We can start with the simplest of physical interactions, and have our robots learn the basics of cause and effect from reflecting on their own experiences. In this experiment, we had the robots play with a wide variety of common household objects by randomly prodding and pushing them inside a tabletop bin. The robots again shared their experiences with each other and together built a single predictive model that attempted to forecast what the world might look like in response to their actions. This predictive model can make simple, if slightly blurry, forecasts about future camera images when provided with the current image and a possible sequence of actions that the robot might execute:
Top row: robotic arms interacting with common household items.
Bottom row: Predicted future camera images given an initial image and a sequence of actions.
Once this model is trained, the robots can use it to perform purposeful manipulations, for example based on user commands. In our prototype, a user can command the robot to move a particular object simply by clicking on that object, and then clicking on the point where the object should go:
The robots in this experiment were not told anything about objects or physics: they only see that the command requires a particular pixel to be moved to a particular place. However, because they have seen so many object interactions in their shared past experiences, they can forecast how particular actions will affect particular pixels. In order for such an implicit understanding of physics to emerge, the robots must be provided with a sufficient breadth of experience. This requires either a lot of time, or sharing the combined experiences of many robots. An extended video on this project may be found here.
Learning with the help of humans.
So far, we discussed how robots can learn entirely on their own. However, human guidance is important, not just for telling the robot what to do, but also for helping the robots along. We have a lot of intuition about how various manipulation skills can be performed, and it only seems natural that transferring this intuition to robots can help them learn these skills a lot faster. In the next experiment, we provided each robot with a different door, and guided each of them by hand to show how these doors can be opened. These demonstrations are encoded into a single combined strategy for all robots, called a policy. The policy is a deep neural network which converts camera images to robot actions, and is maintained on a central server. The following video shows the instructor demonstrating the door-opening skill to a robot:
Next, the robots collectively improve this policy through a trial-and-error learning process. Each robot attempts to open its own door using the latest available policy, with some added noise for exploration. These attempts allow each robot to plan a better strategy for opening the door the next time around, and improve the policy accordingly:
Not surprisingly, we find that robots learn more effectively if they are trained on a curriculum of tasks that are gradually increasing in difficulty. In our experiment, each robot starts off by practicing the door-opening skill on a specific position and orientation of the door that the instructor had previously shown it. As it gets better at performing the task, the instructor starts to alter the position and orientation of the door to be just a bit beyond the current capabilities of the policy, but not so difficult that it fails entirely. This allows the robots to gradually increase their skill level over time, and expands the range of situations they can handle. The combination of human-guidance with trial-and-error learning allowed the robots to collectively learn the skill of door-opening in just a couple of hours. Since the robots were trained on doors that look different from each other, the final policy succeeds on a door with a handle that none of the robots had seen before:
In all three of the experiments described above, the ability to communicate and exchange their experiences allows the robots to learn more quickly and effectively. This becomes particularly important when we combine robotic learning with deep learning, as is the case in all of the experiments discussed above. We’ve seen before that deep learning works best when provided with ample training data. For example, the popular ImageNet benchmark uses over 1.5 million labeled examples. While such a quantity of data is not impossible for a single robot to gather over a few years, it is much more efficient to gather the same volume of experience from multiple robots over the course of a few weeks. Besides faster learning times, this approach might benefit from the greater diversity of experience: a real-world deployment might involve multiple robots in different places and different settings, sharing heterogeneous, varied experiences to build a single highly generalizable representation.

Of course, the kinds of behaviors that robots today can learn are still quite limited. Even basic motion skills, such as picking up objects and opening doors, remain in the realm of cutting edge research. In all of these experiments, a human engineer is still needed to tell the robots what they should learn to do by specifying a detailed objective function. However, as algorithms improve and robots are deployed more widely, their ability to share and pool their experiences could be instrumental for enabling them to assist us in our daily lives.

The experiments on learning by trial-and-error were conducted by Shixiang (Shane) Gu and Ethan Holly from the Google Brain team, and Timothy Lillicrap from DeepMind. Work on learning predictive models was conducted by Chelsea Finn from the Google Brain team, and the research on learning from demonstration was conducted by Yevgen Chebotar, Ali Yahya, Adrian Li, and Mrinal Kalakrishnan from X. We would also like to acknowledge contributions by Peter Pastor, Gabriel Dulac-Arnold, and Jon Scholz. Articles about each of the experiments discussed in this blog post can be found below:

Deep Reinforcement Learning for Robotic Manipulation. Shixiang Gu, Ethan Holly, Timothy Lillicrap, Sergey Levine. [video]

 Deep Visual Foresight for Planning Robot Motion. Chelsea Finn, Sergey Levine. [video] [data]

Collective Robot Reinforcement Learning with Distributed Asynchronous Guided Policy Search.
Ali Yahya, Adrian Li, Mrinal Kalakrishnan, Yevgen Chebotar, Sergey Levine.  [video]

 Path Integral Guided Policy Search. Yevgen Chebotar, Mrinal Kalakrishnan, Ali Yahya, Adrian Li, Stefan Schaal, Sergey Levine. [video]