How does one find a needle in a haystack? At the turn of World War II, that question took on a very concrete form when doctors wondered how to efficiently detect diseases among those who had been drafted into the war effort. Inspired by this challenge, Robert Dorfman, a young statistician at that time (later to become Harvard professor of economics), proposed in a seminal paper a 2-stage approach to detect infected individuals, whereby individual blood samples first are pooled in groups of four before being tested for the presence or absence of a pathogen. If a group is negative, then it is safe to assume that everyone in the group is free of the pathogen. In that case, the reduction in the number of required tests is substantial: an entire group of four people has been cleared with a single test. On the other hand, if a group tests positive, which is expected to happen rarely if the pathogen’s prevalence is small, at least one or more people within that group must be positive; therefore, a few more tests to determine the infected individuals are needed.
information theory, combinatorics or compressive sensing, and several variants of his approach have been proposed, notably those leveraging binary splitting or side knowledge on individual infection probability rates. The field has grown to the extent that several sub-problems are recognized and deserving of an entire literature on their own. Some algorithms are tailored for the noiseless case in which tests are perfectly reliable, whereas some consider instead the more realistic case where tests are noisy and may produce false negatives or positives. Finally, some strategies are adaptive, proposing groups based on test results already observed (including Dorfman’s, since it proposes to re-test individuals that appeared in positive groups), whereas others stick to a non-adaptive setting in which groups are known beforehand or drawn at random.
In “Noisy Adaptive Group Testing using Bayesian Sequential Experimental Design”, we present an approach to group testing that can operate in a noisy setting (i.e., where tests can be mistaken) to decide adaptively by looking at past results which groups to test next, with the goal to converge on a reliable detection as quickly, and with as few tests, as possible. Large scale simulations suggest that this approach may result in significant improvements over both adaptive and non-adaptive baselines, and are far more efficient than individual tests when disease prevalence is low. As such, this approach is particularly well suited for situations that require large numbers of tests to be conducted with limited resources, as may be the case for pandemics, such as that corresponding to the spread of COVID-19. We have open-sourced the code to the community through our GitHub repo.
Noisy and Adaptive Group Testing in a Non-Asymptotic Regime
A group testing strategy is an algorithm that is tasked with guessing who, among a list of n people, carries a particular pathogen. To do so, the strategy provides instructions for pooling individuals into groups. Assuming a laboratory can execute k tests at a time, the strategy will form a k ⨉ n pooling matrix that defines these groups. Once the tests are carried out, the results are used to decide whether sufficient information has been gathered to determine who is or is not infected, and if not, how to form new groups for another round of testing.
We designed a group testing approach for the realistic setting where the testing strategy can be adaptive and where tests are noisy — the probability that the test of an infected sample is positive (sensitivity) is less than 100%, as is the specificity, the probability that a non-infected sample returns negative.
Screening More People with Fewer Tests Using Bayesian Optimal Experimental Design
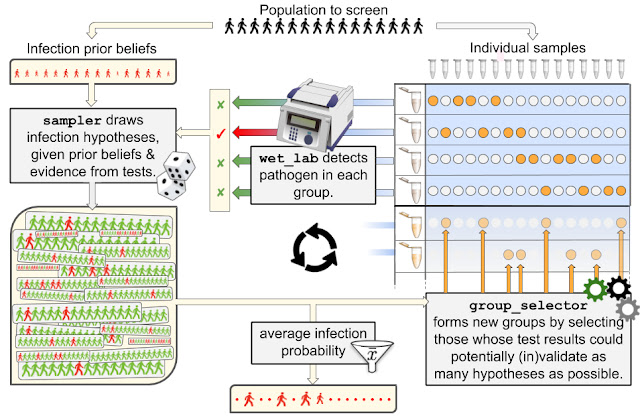
The strategy we propose proceeds the way a detective would investigate a case. They first form several hypotheses about who may or may not be infected, using evidence from all tests (if any) that have been carried out so far and prior information on the infection rate (a). Using these hypotheses, our detectives produce an actionable item to continue the investigation, namely a next wave of groups that may help in validating or invalidating as many hypotheses as possible (b), and then loop back to (a) until the set of plausible hypotheses is small enough to unambiguously identify the target of the search. More precisely,
- Given a population of n people, an infection state is a binary vector of length n that describes who is infected (marked with a 1), and who is not (marked with a 0). At a certain time, a population is in a given state (most likely a few 1’s and mostly 0’s). The goal of group testing is to identify that state using as few tests as possible. Given a prior belief on the infection rate (the disease is rare) and test results observed so far (if any), we expect that only a small share of those infection states will be plausible. Rather than evaluating the plausibility of all 2n possible states (an extremely large number even for small n), we resort to a more efficient method to sample plausible hypotheses using a sequential Monte Carlo (SMC) sampler. Although quite costly by common standards (a few minutes using a GPU in our experimental setup), we show in this work that SMC samplers remain tractable even for large n, opening new possibilities for group testing. In short, in return for a few minutes of computations, our detectives get an extensive list of thousands of relevant hypotheses that may explain tests observed so far.
- Equipped with a relevant list of hypotheses, our strategy proceeds, as detectives would, by selectively gathering additional evidence. If k tests can be carried out at the next iteration, our strategy will propose to test k new groups, which are computed using the framework of Bayesian optimal experimental design. Intuitively, if k=1 and one can only propose a single new group to test, there would be clear advantage in building that group such that its test outcome is as uncertain as possible, i.e., with a probability that it returns positive as close to 50% as possible, given the current set of hypotheses. Indeed, to progress in an investigation, it is best to maximize the surprise factor (or information gain) provided by new test results, as opposed to using them to confirm further what we already hold to be very likely. To generalize that idea to a set of k>1 new groups, we score this surprise factor by computing the mutual information of these “virtual” group tests vs. the distribution of hypotheses. We also consider a more involved approach that computes the expected area under the ROC curve (AUC) one would obtain from testing these new groups using the distribution of hypotheses. The maximization of these two criteria is carried out using a greedy approach, resulting in two group selectors, GMIMAX and GAUCMAX (greedy maximization of mutual information or AUC, respectively).
wet_lab) carrying out testing, and our strategy, composed of a sampler and a group selector, is summarized in the following drawing, which uses names of classes implemented in our open source package. We benchmarked our two strategies GMIMAX and GAUCMAX against various baselines in a wide variety of settings (infection rates, test noise levels), reporting performance as the number of tests increases. In addition to simple Dorfman strategies, the baselines we considered included a mix of non-adaptive strategies (origami assays, random designs) complemented at later stages with the so-called informative Dorfman approach. Our approaches significantly outperform the others in all settings.
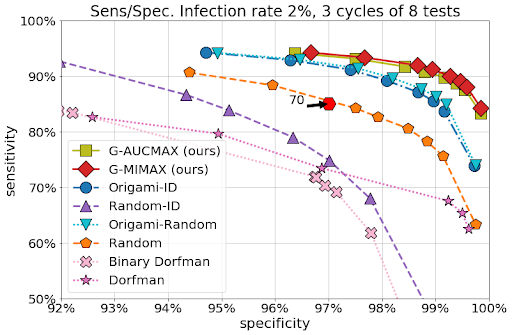 |
| We executed 5000 simulations on a sample population of 70 individuals with an infection rate of 2%. We have assumed sensitivity/specificity values of 85% / 97% for tests with groups of maximal size 10, which are representative of current PCR machines. This figure demonstrates that our approach outperforms the other baselines with as few as 24 tests (up to 8 tests used in 3 cycles), including both adaptive and non-adaptive varieties, and performs significantly better than individual tests (plotted in the sensitivity/specificity plane as a hexagon, requiring 70 tests), highlighting the savings potential offered by group testing. See preprint for other setups. |
Screening a population for a pathogen is a fundamental problem, one that we currently face during the current COVID-19 epidemic. Seventy years ago, Dorfman proposed a simple approach currently adopted by various institutions. Here, we have proposed a method to extend the basic group testing approach in several ways. Our first contribution is to adopt a probabilistic perspective, and form thousands of plausible hypotheses of infection distributions given test outcomes, rather than trust test results to be 100% reliable as Dorfman did. This perspective allows us to seamlessly incorporate additional prior knowledge on infection, such as when we suspect some individuals to be more likely than others to carry the pathogen, based for instance on contact tracing data or answers to a questionnaire. This provides our algorithms, which can be compared to detectives investigating a case, the advantage of knowing what are the most likely infection hypotheses that agree with prior beliefs and tests carried out so far. Our second contribution is to propose algorithms that can take advantage of these hypotheses to form new groups, and therefore direct the gathering of new evidence, to narrow down as quickly as possible to the "true" infection hypothesis, and close the case with as little testing effort as possible.
Acknowledgements
We would like to thank our collaborators on this work, Olivier Teboul, in particular, for his help preparing figures, as well as Arnaud Doucet and Quentin Berthet. We also thank Kevin Murphy and Olivier Bousquet (Google) for their suggestions at the earliest stages of this project, as well as Dan Popovici for his unwavering support pushing this forward; Ignacio Anegon, Jeremie Poschmann and Laurent Tesson (INSERM) for providing us background information on RT-PCR tests and Nicolas Chopin (CREST) for giving guidance on his work to define SMCs for binary spaces.