Relational data representing relationships between entities is ubiquitous on the Web (e.g., online social networks) and in the physical world (e.g., in protein interaction networks). Such data can be represented as a graph with nodes (e.g., users, proteins), and edges connecting them (e.g., friendship relations, protein interactions). Given the widespread prevalence of graphs, graph analysis plays a fundamental role in machine learning, with applications in clustering, link prediction, privacy, and others. To apply machine learning methods to graphs (e.g., predicting new friendships, or discovering unknown protein interactions) one needs to learn a representation of the graph that is amenable to be used in ML algorithms.
However, graphs are inherently combinatorial structures made of discrete parts like nodes and edges, while many common ML methods, like neural networks, favor continuous structures, in particular vector representations. Vector representations are particularly important in neural networks, as they can be directly used as input layers. To get around the difficulties in using discrete graph representations in ML, graph embedding methods learn a continuous vector space for the graph, assigning each node (and/or edge) in the graph to a specific position in a vector space. A popular approach in this area is that of random-walk-based representation learning, as introduced in DeepWalk.
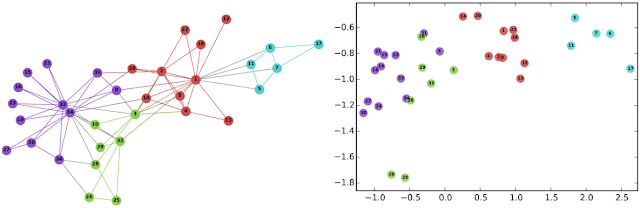 |
| Left: The well-known Karate graph representing a social network. Right: A continuous space embedding of the nodes in the graph using DeepWalk. |
Learning Node Representations that Capture Multiple Social Contexts
In virtually all cases, the crucial assumption of standard graph embedding methods is that a single embedding has to be learned for each node. Thus, the embedding method can be said to seek to identify the single role or position that characterizes each node in the geometry of the graph. Recent work observed, however, that nodes in real networks belong to multiple overlapping communities and play multiple roles—think about your social network where you participate in both your family and in your work community. This observation motivates the following research question: is it possible to develop methods where nodes are embedded in multiple vectors, representing their participation in overlapping communities?
In our WWW’19 paper, we developed Splitter, an unsupervised embedding method that allows the nodes in a graph to have multiple embeddings to better encode their participation in multiple communities. Our method is based on recent innovations in overlapping clustering based on ego-network analysis, using the persona graph concept, in particular. This method takes a graph G, and creates a new graph P (called the persona graph), where each node in G is represented by a series of replicas called the persona nodes. Each persona of a node represents an instantiation of the node in a local community to which it belongs. For each node U in the graph, we analyze the ego-network of the node (i.e., the graph connecting the node to its neighbors, in this example A, B, C, D) to discover local communities to which the node belongs. For instance, in the figure below, node U belongs to two communities: Cluster 1 (with the friends A and B, say U’s family members) and Cluster 2 (with C and D, say U’s colleagues).
 |
| Ego-net of node U |
 |
| The ego-splitting method separating the U nodes in 2 personas. |
 |
| Top Left: A typical graphs with highly overlapping communities. Top Right: A traditional embedding of the graph on the left using node2vec. Bottom Left: A persona graph of the graph above. Bottom Right: The Splitter embedding of the persona graph. Notice how the persona graph clearly disentangles the overlapping communities of the original graph and Splitter outputs well-separated embeddings. |
Graph embedding methods have shown outstanding performance on various ML-based applications, such as link prediction and node classification, but they have a number of hyper-parameters that must be manually set. For example, are nearby nodes more important to capture when learning embeddings than nodes that are further away? Even though experts may be able to fine tune these hyper-parameters, one must do so independently for each graph. To obviate such manual work, in our second paper, we proposed a method to learn the optimal hyper-parameters automatically.
Specifically, many graph embedding methods, like DeepWalk, employ random walks to explore the context around a given node (i.e. the direct neighbors, the neighbors of the neighbors, etc). Such random walks can have many hyper-parameters that allow tuning of the local exploration of the graph, thus regulating the attention given by the embeddings to nearby nodes. Different graphs may present different optimal attention patterns and hence different optimal hyperparameters (see the picture below, where we show two different attention distributions). Watch Your Step formulates a model for the performance of the embedding methods based on the above mentioned hyper-parameters. Then we optimize the hyper-parameters to maximize the performance predicted by the model, using standard backpropagation. We found that the values learned by backpropagation agree with the optimal hyper-parameters obtained by grid search.
AutoML, where we want to alleviate the burden of optimizing the hyperparameters—a common problem in practical machine learning. Many AutoML methods use neural architecture search. This paper instead shows a variant, where we use the mathematical connection between the hyperparameters in the embeddings and graph-theoretic matrix formulations. The “Auto” portion corresponds to learning the graph hyperparameters by backpropagation.
We believe that our contributions will further advance the state of the research in graph embedding in various directions. Our method for learning multiple node embeddings draws a connection between the rich and well-studied field of overlapping community detection, and the more recent one of graph embedding which we believe may result in fruitful future research. An open problem in this area is the use of multiple-embedding methods for classification. Furthermore, our contribution on learning hyperparameters will foster graph embedding adoption by reducing the need for expensive manual tuning. We hope the release of these papers and code will help the research community pursue these directions.
Acknowledgements
We thank Sami Abu-el-Haija who contributed to this work and is now a Ph.D. student at USC.
