Tag Archives: Graph

Google Research, 2022 & beyond: Algorithmic advances

Posted by Vahab Mirrokni, VP and Google Fellow, Google Research

(This is Part 5 in our series of posts covering different topical areas of research at Google. You can find other posts in the series here.)

Robust algorithm design is the backbone of systems across Google, particularly for our ML and AI models. Hence, developing algorithms with improved efficiency, performance and speed remains a high priority as it empowers services ranging from Search and Ads to Maps and YouTube. Google Research has been at the forefront of this effort, developing many innovations from privacy-safe recommendation systems to scalable solutions for large-scale ML. In 2022, we continued this journey, and advanced the state-of-the-art in several related areas. Here we highlight our progress in a subset of these, including scalability, privacy, market algorithms, and algorithmic foundations.




Scalable algorithms: Graphs, clustering, and optimization

As the need to handle large-scale datasets increases, scalability and reliability of complex algorithms that also exhibit improved explainability, robustness, and speed remain a high priority. We continued our efforts in developing new algorithms for handling large datasets in various areas, including unsupervised and semi-supervised learning, graph-based learning, clustering, and large-scale optimization.

An important component of such systems is to build a similarity graph — a nearest-neighbor graph that represents similarities between objects. For scalability and speed, this graph should be sparse without compromising quality. We proposed a 2-hop spanner technique, called STAR, as an efficient and distributed graph building strategy, and showed how it significantly decreases the number of similarity computations in theory and practice, building much sparser graphs while producing high-quality graph learning or clustering outputs. As an example, for graphs with 10T edges, we demonstrate ~100-fold improvements in pairwise similarity comparisons and significant running time speedups with negligible quality loss. We had previously applied this idea to develop massively parallel algorithms for metric, and minimum-size clustering. More broadly in the context of clustering, we developed the first linear-time hierarchical agglomerative clustering (HAC) algorithm as well as DBSCAN, the first parallel algorithm for HAC with logarithmic depth, which achieves 50x speedup on 100B-edge graphs. We also designed improved sublinear algorithms for different flavors of clustering problems such as geometric linkage clustering, constant-round correlation clustering, and fully dynamic k-clustering.

Inspired by the success of multi-core processing (e.g., GBBS), we embarked on a mission to develop graph mining algorithms that can handle graphs with 100B edges on a single multi-core machine. The big challenge here is to achieve fast (e.g., sublinear) parallel running time (i.e., depth). Following our previous work for community detection and correlation clustering, we developed an algorithm for HAC, called ParHAC, which has provable polylogarithmic depth and near-linear work and achieves a 50x speedup. As an example, it took ParHAC only ~10 minutes to find an approximate affinity hierarchy over a graph of over 100B edges, and ~3 hours to find the full HAC on a single machine. Following our previous work on distributed HAC, we use these multi-core algorithms as a subroutine within our distributed algorithms in order to handle tera-scale graphs.

We also had a number of interesting results on graph neural networks (GNN) in 2022. We provided a model-based taxonomy that unified many graph learning methods. In addition, we discovered insights for GNN models from their performance across thousands of graphs with varying structure (shown below). We also proposed a new hybrid architecture to overcome the depth requirements of existing GNNs for solving fundamental graph problems, such as shortest paths and the minimum spanning tree.

Relative performance results of three GNN variants (GCN, APPNP, FiLM) across 50,000 distinct node classification datasets in GraphWorld. We find that academic GNN benchmark datasets exist in regions where model rankings do not change. GraphWorld can discover previously unexplored graphs that reveal new insights about GNN architectures.

Furthermore, to bring some of these many advances to the broader community, we had three releases of our flagship modeling library for building graph neural networks in TensorFlow (TF-GNN). Highlights include a model library and model orchestration API to make it easy to compose GNN solutions. Following our NeurIPS’20 workshop on Mining and Learning with Graphs at Scale, we ran a workshop on graph-based learning at ICML’22, and a tutorial for GNNs in TensorFlow at NeurIPS’22.

In “Robust Routing Using Electrical Flows”, we presented a recent paper that proposed a Google Maps solution to efficiently compute alternate paths in road networks that are resistant to failures (e.g., closures, incidents). We demonstrate how it significantly outperforms the state-of-the-art plateau and penalty methods on real-world road networks.

Example of how we construct the electrical circuit corresponding to the road network. The current can be decomposed into three flows, i1, i2 and i3, each of which corresponds to a viable alternate path from Fremont, CA to San Rafael, CA.

On the optimization front, we open-sourced Vizier, our flagship blackbox optimization and hyperparameter tuning library at Google. We also developed new techniques for linear programming (LP) solvers that address scalability limits caused by their reliance on matrix factorizations, which restricts the opportunity for parallelism and distributed approaches. To this end, we open-sourced a primal-dual hybrid gradient (PDHG) solution for LP called primal-dual linear programming (PDLP), a new first-order solver for large-scale LP problems. PDLP has been used to solve real-world problems with as many as 12B non-zeros (and an internal distributed version scaled to 92B non-zeros). PDLP's effectiveness is due to a combination of theoretical developments and algorithm engineering.

With OSS Vizier, multiple clients each send a “Suggest” request to the Service API, which produces Suggestions for the clients using Pythia policies. The clients evaluate these suggestions and return measurements. All transactions are stored to allow fault-tolerance.

Top


Privacy and federated learning

Respecting user privacy while providing high-quality services remains a top priority for all Google systems. Research in this area spans many products and uses principles from differential privacy (DP) and federated learning.

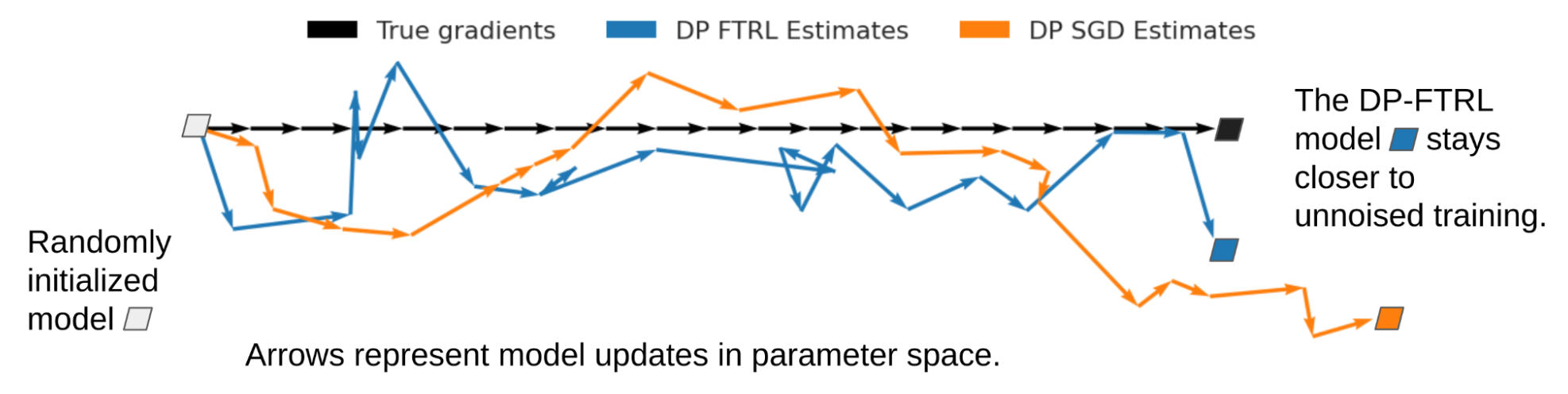
First of all, we have made a variety of algorithmic advances to address the problem of training large neural networks with DP. Building on our earlier work, which enabled us to launch a DP neural network based on the DP-FTRL algorithm, we developed the matrix factorization DP-FTRL approach. This work demonstrates that one can design a mathematical program to optimize over a large set of possible DP mechanisms to find those best suited for specific learning problems. We also establish margin guarantees that are independent of the input feature dimension for DP learning of neural networks and kernel-based methods. We further extend this concept to a broader range of ML tasks, matching baseline performance with 300x less computation. For fine-tuning of large models, we argued that once pre-trained, these models (even with DP) essentially operate over a low-dimensional subspace, hence circumventing the curse of dimensionality that DP imposes.

On the algorithmic front, for estimating the entropy of a high-dimensional distribution, we obtained local DP mechanisms (that work even when as little as one bit per sample is available) and efficient shuffle DP mechanisms. We proposed a more accurate method to simultaneously estimate the top-k most popular items in the database in a private manner, which we employed in the Plume library. Moreover, we showed a near-optimal approximation algorithm for DP clustering in the massively parallel computing (MPC) model, which further improves on our previous work for scalable and distributed settings.

Another exciting research direction is the intersection of privacy and streaming. We obtained a near-optimal approximation-space trade-off for the private frequency moments and a new algorithm for privately counting distinct elements in the sliding window streaming model. We also presented a general hybrid framework for studying adversarial streaming.

Addressing applications at the intersection of security and privacy, we developed new algorithms that are secure, private, and communication-efficient, for measuring cross-publisher reach and frequency. The World Federation of Advertisers has adopted these algorithms as part of their measurement system. In subsequent work, we developed new protocols that are secure and private for computing sparse histograms in the two-server model of DP. These protocols are efficient from both computation and communication points of view, are substantially better than what standard methods would yield, and combine tools and techniques from sketching, cryptography and multiparty computation, and DP.

While we have trained BERT and transformers with DP, understanding training example memorization in large language models (LLMs) is a heuristic way to evaluate their privacy. In particular, we investigated when and why LLMs forget (potentially memorized) training examples during training. Our findings suggest that earlier-seen examples may observe privacy benefits at the expense of examples seen later. We also quantified the degree to which LLMs emit memorized training data.

Top


Market algorithms and causal inference

We also continued our research in improving online marketplaces in 2022. For example, an important recent area in ad auction research is the study of auto-bidding online advertising where the majority of bidding happens via proxy bidders that optimize higher-level objectives on behalf of advertisers. The complex dynamics of users, advertisers, bidders, and ad platforms leads to non-trivial problems in this space. Following our earlier work in analyzing and improving mechanisms under auto-bidding auctions, we continued our research in improving online marketplaces in the context of automation while taking different aspects into consideration, such as user experience and advertiser budgets. Our findings suggest that properly incorporating ML advice and randomization techniques, even in non-truthful auctions, can robustly improve the overall welfare at equilibria among auto-bidding algorithms.

Structure of auto-bidding online ads system.

Beyond auto-bidding systems, we also studied auction improvements in complex environments, e.g., settings where buyers are represented by intermediaries, and with Rich Ads where each ad can be shown in one of several possible variants. We summarize our work in this area in a recent survey. Beyond auctions, we also investigate the use of contracts in multi-agent and adversarial settings.

Online stochastic optimization remains an important part of online advertising systems with application in optimal bidding and budget pacing. Building on our long-term research in online allocation, we recently blogged about dual mirror descent, a new algorithm for online allocation problems that is simple, robust, and flexible. This state-of-the-art algorithm is robust against a wide range of adversarial and stochastic input distributions and can optimize important objectives beyond economic efficiency, such as fairness. We also show that by tailoring dual mirror descent to the special structure of the increasingly popular return-on-spend constraints, we can optimize advertiser value. Dual mirror descent has a wide range of applications and has been used over time to help advertisers obtain more value through better algorithmic decision making.

An overview of the dual mirror descent algorithm.

Furthermore, following our recent work at the interplay of ML, mechanism design and markets, we investigated transformers for asymmetric auction design, designed utility-maximizing strategies for no-regret learning buyers, and developed new learning algorithms to bid or to price in auctions.

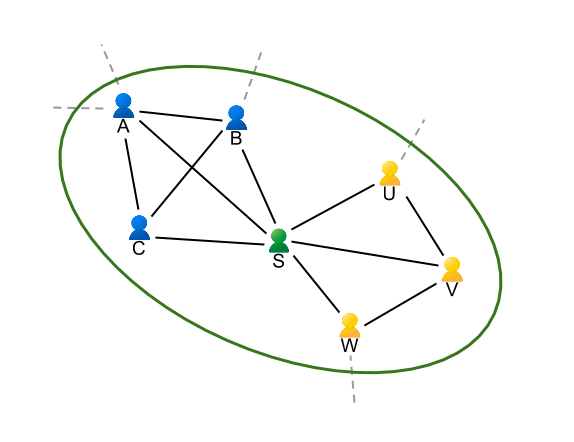
An overview of bipartite experimental design to reduce causal interactions between entities.

A critical component of any sophisticated online service is the ability to experimentally measure the response of users and other players to new interventions. A major challenge of estimating these causal effects accurately is handling complex interactions — or interference — between the control and treatment units of these experiments. We combined our graph clustering and causal inference expertise to expand the results of our previous work in this area, with improved results under a flexible response model and a new experimental design that is more effective at reducing these interactions when treatment assignments and metric measurements occur on the same side of a bipartite platform. We also showed how synthetic control and optimization techniques can be combined to design more powerful experiments, especially in small data regimes.

Top


Algorithmic foundations and theory

Finally, we continued our fundamental algorithmic research by tackling long-standing open problems. A surprisingly concise paper affirmatively resolved a four-decade old open question on whether there is a mechanism that guarantees a constant fraction of the gains-from-trade attainable whenever buyer's value weakly exceeds seller's cost. Another recent paper obtained the state-of-the-art approximation for the classic and highly-studied k-means problem. We also improved the best approximation for correlation clustering breaking the barrier approximation factor of 2. Finally, our work on dynamic data structures to solve min-cost and other network flow problems has contributed to a breakthrough line of work in adapting continuous optimization techniques to solve classic discrete optimization problems.

Top


Concluding thoughts

Designing effective algorithms and mechanisms is a critical component of many Google systems that need to handle tera-scale data robustly with critical privacy and safety considerations. Our approach is to develop algorithms with solid theoretical foundations that can be deployed effectively in our product systems. In addition, we are bringing many of these advances to the broader community by open-sourcing some of our most novel developments and by publishing the advanced algorithms behind them. In this post, we covered a subset of algorithmic advances in privacy, market algorithms, scalable algorithms, graph-based learning, and optimization. As we move toward an AI-first Google with further automation, developing robust, scalable, and privacy-safe ML algorithms remains a high priority. We are excited about developing new algorithms and deploying them more broadly.



Acknowledgements

This post summarizes research from a large number of teams and benefited from input from several researchers including Gagan Aggarwal, Amr Ahmed, David Applegate, Santiago Balseiro, Vincent Cohen-addad, Yuan Deng, Alessandro Epasto, Matthew Fahrbach, Badih Ghazi, Sreenivas Gollapudi, Rajesh Jayaram, Ravi Kumar, Sanjiv Kumar, Silvio Lattanzi, Kuba Lacki, Brendan McMahan, Aranyak Mehta, Bryan Perozzi, Daniel Ramage, Ananda Theertha Suresh, Andreas Terzis, Sergei Vassilvitskii, Di Wang, and Song Zuo. Special thanks to Ravi Kumar for his contributions to this post.


Google Research, 2022 & beyond

This was the fifth blog post in the “Google Research, 2022 & Beyond” series. Other posts in this series are listed in the table below:


Language Models Computer Vision Multimodal Models
Generative Models Responsible AI ML & Computer Systems
Efficient Deep Learning Algorithmic Advances Robotics*
Health General Science & Quantum Community Engagement

* Articles will be linked as they are released.

Source: Google AI Blog


JanusGraph connects the past and future of Titan

We are thrilled to collaborate with a group of individuals and companies, including Expero, GRAKN.AI, Hortonworks and IBM, in launching a new project — JanusGraph — under The Linux Foundation to advance the state-of-the-art in distributed graph computation.



JanusGraph is a fork of the popular open source project Titan, originally released in 2012 by Aurelius, and subsequently acquired by DataStax. Titan has been widely adopted for large-scale distributed graph computation and many users have contributed to its ongoing development, which has slowed down as of late: there have been no Titan releases since the 1.0 release in September 2015, and the repository has seen no updates since June 2016.

This new project will reinvigorate development of the distributed graph system to add new functionality, improve performance and scalability, and maintain a variety of storage backends.

The name "Janus" comes from the name of a Roman god who looks simultaneously into the past to the Titans (divine beings from Greek mythology) as well as into the future.

All are welcome to participate in the JanusGraph project, whether by contributing features or bug fixes, filing feature requests and bugs, improving the documentation or helping shape the product roadmap through feature requests and use cases.

Get involved by taking a look at our website and browse the code on GitHub.

We look forward to hearing from you!

By Misha Brukman, Google Cloud Platform

Graph-powered Machine Learning at Google

Posted by Sujith Ravi, Staff Research Scientist, Google Research

Recently, there have been significant advances in Machine Learning that enable computer systems to solve complex real-world problems. One of those advances is Google’s large scale, graph-based machine learning platform, built by the Expander team in Google Research. A technology that is behind many of the Google products and features you may use everyday, graph-based machine learning is a powerful tool that can be used to power useful features such as reminders in Inbox and smart messaging in Allo, or used in conjunction with deep neural networks to power the latest image recognition system in Google Photos.
Learning with Minimal Supervision

Much of the recent success in deep learning and machine learning, in general, can be attributed to models that demonstrate high predictive capacity when trained on large amounts of labeled data -- often millions of training examples. This is commonly referred to as “supervised learning” since it requires supervision, in the form of labeled data, to train the machine learning systems. (Conversely, some machine learning methods operate directly on raw data without any supervision, a paradigm referred to as unsupervised learning.)

However, the more difficult the task, the harder it is to get sufficient high-quality labeled data. It is often prohibitively labor intensive and time-consuming to collect labeled data for every new problem. This motivated the Expander research team to build new technology for powering machine learning applications at scale and with minimal supervision.

Expander’s technology draws inspiration from how humans learn to generalize and bridge the gap between what they already know (labeled information) and novel, unfamiliar observations (unlabeled information). Known as “semi-supervised” learning, this powerful technique enables us to build systems that can work in situations where training data may be sparse. One of the key advantages to a graph-based semi-supervised machine learning approach is the fact that (a) one models labeled and unlabeled data jointly during learning, leveraging the underlying structure in the data, (b) one can easily combine multiple types of signals (for example, relational information from Knowledge Graph along with raw features) into a single graph representation and learn over them. This is in contrast to other machine learning approaches, such as neural network methods, in which it is typical to first train a system using labeled data with features and then apply the trained system to unlabeled data.

Graph Learning: How It Works

At its core, Expander’s platform combines semi-supervised machine learning with large-scale graph-based learning by building a multi-graph representation of the data with nodes corresponding to objects or concepts and edges connecting concepts that share similarities. The graph typically contains both labeled data (nodes associated with a known output category or label) and unlabeled data (nodes for which no labels were provided). Expander’s framework then performs semi-supervised learning to label all nodes jointly by propagating label information across the graph.

However, this is easier said than done! We have to (1) learn efficiently at scale with minimal supervision (i.e., tiny amount of labeled data), (2) operate over multi-modal data (i.e., heterogeneous representations and various sources of data), and (3) solve challenging prediction tasks (i.e., large, complex output spaces) involving high dimensional data that might be noisy.

One of the primary ingredients in the entire learning process is the graph and choice of connections. Graphs come in all sizes, shapes and can be combined from multiple sources. We have observed that it is often beneficial to learn over multi-graphs that combine information from multiple types of data representations (e.g., image pixels, object categories and chat response messages for PhotoReply in Allo). The Expander team’s graph learning platform automatically generates graphs directly from data based on the inferred or known relationships between data elements. The data can be structured (for example, relational data) or unstructured (for example, sparse or dense feature representations extracted from raw data).

To understand how Expander’s system learns, let us consider an example graph shown below.
There are two types of nodes in the graph: “grey” represents unlabeled data whereas the colored nodes represent labeled data. Relationships between node data is represented via edges and thickness of each edge indicates strength of the connection. We can formulate the semi-supervised learning problem on this toy graph as follows: predict a color (“red” or “blue”) for every node in the graph. Note that the specific choice of graph structure and colors depend on the task. For example, as shown in this research paper we recently published, a graph that we built for the Smart Reply feature in Inbox represents email messages as nodes and colors indicate semantic categories of user responses (e.g., “yes”, “awesome”, “funny”).

The Expander graph learning framework solves this labeling task by treating it as an optimization problem. At the simplest level, it learns a color label assignment for every node in the graph such that neighboring nodes are assigned similar colors depending on the strength of their connection. A naive way to solve this would be to try to learn a label assignment for all nodes at once -- this method does not scale to large graphs. Instead, we can optimize the problem formulation by propagating colors from labeled nodes to their neighbors, and then repeating the process. In each step, an unlabeled node is assigned a label by inspecting color assignments of its neighbors. We can update every node’s label in this manner and iterate until the whole graph is colored. This process is a far more efficient way to optimize the same problem and the sequence of iterations converges to a unique solution in this case. The solution at the end of the graph propagation looks something like this:
Semi-supervised learning on a graph
In practice, we use complex optimization functions defined over the graph structure, which incorporate additional information and constraints for semi-supervised graph learning that can lead to hard, non-convex problems. The real challenge, however, is to scale this efficiently to graphs containing billions of nodes, trillions of edges and for complex tasks involving billions of different label types.

To tackle this challenge, we created an approach outlined in Large Scale Distributed Semi-Supervised Learning Using Streaming Approximation, published last year. It introduces a streaming algorithm to process information propagated from neighboring nodes in a distributed manner that makes it work on very large graphs. In addition, it addresses other practical concerns, notably it guarantees that the space complexity or memory requirements of the system stays constant regardless of the difficulty of the task, i.e., the overall system uses the same amount of memory regardless of whether the number of prediction labels is two (as in the above toy example) or a million or even a billion. This enables wide-ranging applications for natural language understanding, machine perception, user modeling and even joint multimodal learning for tasks involving multiple modalities such as text, image and video inputs.

Language Graphs for Learning Humor

As an example use of graph-based machine learning, consider emotion labeling, a language understanding task in Smart Reply for Inbox, where the goal is to label words occurring in natural language text with their fine-grained emotion categories. A neural network model is first applied to a text corpus to learn word embeddings, i.e., a mathematical vector representation of the meaning of each word. The dense embedding vectors are then used to build a sparse graph where nodes correspond to words and edges represent semantic relationship between them. Edge strength is computed using similarity between embedding vectors — low similarity edges are ignored. We seed the graph with emotion labels known a priori for a few nodes (e.g., laugh is labeled as “funny”) and then apply semi-supervised learning over the graph to discover emotion categories for remaining words (e.g., ROTFL gets labeled as “funny” owing to its multi-hop semantic connection to the word “laugh”).
Learning emotion associations using graph constructed from word embedding vectors
For applications involving large datasets or dense representations that are observed (e.g., pixels from images) or learned using neural networks (e.g., embedding vectors), it is infeasible to compute pairwise similarity between all objects to construct edges in the graph. The Expander team solves this problem by leveraging approximate, linear-time graph construction algorithms.

Graph-based Machine Intelligence in Action

The Expander team’s machine learning system is now being used on massive graphs (containing billions of nodes and trillions of edges) to recognize and understand concepts in natural language, images, videos, and queries, powering Google products for applications like reminders, question answering, language translation, visual object recognition, dialogue understanding, and more.

We are excited that with the recent release of Allo, millions of chat users are now experiencing smart messaging technology powered by the Expander team’s system for understanding and assisting with chat conversations in multiple languages. Also, this technology isn’t used only for large-scale models in the cloud - as announced this past week, Android Wear has opened up an on-device Smart Reply capability for developers that will provide smart replies for any messaging application. We’re excited to tackle even more challenging Internet-scale problems with Expander in the years to come.

Acknowledgements

We wish to acknowledge the hard work of all the researchers, engineers, product managers, and leaders across Google who helped make this technology a success. In particular, we would like to highlight the efforts of Allan Heydon, Andrei Broder, Andrew Tomkins, Ariel Fuxman, Bo Pang, Dana Movshovitz-Attias, Fritz Obermeyer, Krishnamurthy Viswanathan, Patrick McGregor, Peter Young, Robin Dua, Sujith Ravi and Vivek Ramavajjala.

The 280-Year-Old Algorithm Inside Google Trips

Posted by Bogdan Arsintescu, Software Engineer & Sreenivas Gollapudi, Kostas Kollias, Tamas Sarlos and Andrew Tomkins, Research Scientists


Algorithms Engineering is a lot of fun because algorithms do not go out of fashion: one never knows when an oldie-but-goodie might come in handy. Case in point: Yesterday, Google announced Google Trips, a new app to assist you in your travels by helping you create your own “perfect day” in a city. Surprisingly, deep inside Google Trips, there is an algorithm that was invented 280 years ago.

In 1736, Leonhard Euler authored a brief but beautiful mathematical paper regarding the town of Königsberg and its 7 bridges, shown here:
Image from Wikipedia
In the paper, Euler studied the following question: is it possible to walk through the city crossing each bridge exactly once? As it turns out, for the city of Königsberg, the answer is no. To reach this answer, Euler developed a general approach to represent any layout of landmasses and bridges in terms of what he dubbed the Geometriam Situs (the “Geometry of Place”), which we now call Graph Theory. He represented each landmass as a “node” in the graph, and each bridge as an “edge,” like this:
Image from Wikipedia
Euler noticed that if all the nodes in the graph have an even number of edges (such graphs are called “Eulerian” in his honor) then, and only then, a cycle can be found that visits every edge exactly once. Keep this in mind, as we’ll rely on this fact later in the post.

Our team in Google Research has been fascinated by the “Geometry of Place” for some time, and we started investigating a question related to Euler’s: rather than visiting just the bridges, how can we visit as many interesting places as possible during a particular trip? We call this the “itineraries” problem. Euler didn’t study it, but it is a well known topic in Optimization, where it is often called the “Orienteering” problem.

While Euler’s problem has an efficient and exact solution, the itineraries problem is not just hard to solve, it is hard to even approximately solve! The difficulty lies in the interplay between two conflicting goals: first, we should pick great places to visit, but second, we should pick them to allow a good itinerary: not too much travel time; don’t visit places when they’re closed; don’t visit too many museums, etc. Embedded in such problems is the challenge of finding efficient routes, often referred to as the Travelling Salesman Problem (TSP).

Algorithms for Travel Itineraries

Fortunately, the real world has a property called the “triangle inequality” that says adding an extra stop to a route never makes it shorter. When the underlying geometry satisfies the triangle inequality, the TSP can be approximately solved using another algorithm discovered by Christofides in 1976. This is an important part of our solution, and builds on Euler’s paper, so we’ll give a quick four-step rundown of how it works here:
  1. We start with all our destinations separate, and repeatedly connect together the closest two that aren’t yet connected. This doesn’t yet give us an itinerary, but it does connect all the destinations via a minimum spanning tree of the graph.
  2. We take all the destinations that have an odd number of connections in this tree (Euler proved there must be an even number of these), and carefully pair them up.
  3. Because all the destinations now have an even number of edges, we’ve created an Eulerian graph, so we create a route that crosses each edge exactly once.
  4. We now have a great route, but it might visit some places more than once. No problem, we find any double visits and simply bypass them, going directly from the predecessor to the successor.
Christofides gave an elegant proof that the resulting route is always close to the shortest possible. Here’s an example of the Christofides’ algorithm in action on a location graph with the nodes representing places and the edges with costs representing the travel time between the places.
Construction of an Eulerian Tour in a location graph
Armed with this efficient route-finding subroutine, we can now start building itineraries one step at a time. At each step, we estimate the benefit to the user of each possible new place to visit, and likewise estimate the cost using the Christofides algorithm. A user’s benefit can be derived from a host of natural factors such as the popularity of the place and how different the place is relative to places already visited on the tour. We then pick whichever new place has the best benefit per unit of extra cost (e.g., time needed to include the new place in the tour). Here’s an example of our algorithm actually building a route in London using the location graph shown above:
Itineraries in Google Trips

With our first good approximate solution to the itineraries problem in hand, we started working with our colleagues from the Google Trips team, and we realized we’d barely scratched the surface. For instance, even if we produce the absolute perfect itinerary, any particular user of the system will very reasonably say, “That’s great, but all my friends say I also need to visit this other place. Plus, I’m only around for the morning, and I don’t want to miss this place you listed in the afternoon. And I’ve already seen Big Ben twice.” So rather than just producing an itinerary once and calling it a perfect day, we needed a fast dynamic algorithm for itineraries that users can modify on the fly to suit their individual taste. And because many people have bad data connections while traveling, the solution had to be efficient enough to run disconnected on a phone.

Better Itineraries Through the Wisdom of Crowds

While the algorithmic aspects of the problem were highly challenging, we realized that producing high-quality itineraries was just as dependent on our understanding of the many possible stopping points on the itinerary. We had Google’s extensive travel database to identify the interesting places to visit, and we also had great data from Google’s existing systems about how to travel from any place to any other. But we didn’t have a good sense for how people typically move through this geometry of places.

For this, we turned to the wisdom of crowds. This type of wisdom is used by Google to estimate delays on highways, and to discover when restaurants are most busy. Here, we use the same techniques to learn about common visit sequences that we can stitch together into itineraries that feel good to our users. We combine Google's knowledge of when places are popular, with the directions between those places to gather an idea of what tourists like to do when travelling.

And the crowd has a lot more wisdom to offer in the future. For example, we noticed that visits to Buckingham Palace spike around 11:30 and stay a bit longer than at other times of the day. This seemed a little strange to us, but when we looked more closely, it turns out to be the time of the Changing of the Guard. We’re looking now at ways to incorporate this type of timing information into the itinerary selection algorithms.

So give it a try: Google Trips, available now on Android and iOS, has you covered from departure to return.

Research from VLDB 2016: Improved Friend Suggestion using Ego-Net Analysis

Posted by Alessandro Epasto, Research Scientist, Google Research NY

On September 5 - 9, New Delhi, India hosted the 42nd International Conference on Very Large Data Bases (VLDB), a premier annual forum for academic and industry research on databases, data management, data mining and data analytics. Over the past several years, Google has actively participated in VLDB, both as official sponsor and with numerous contributions to the research and industrial tracks. In this post, we would like to share the research presented in one of the Google papers from VLDB 2016.

In Ego-net Community Mining Applied to Friend Suggestion, co-authored by Googlers Silvio Lattanzi, Vahab Mirrokni, Ismail Oner Sebe, Ahmed Taei, Sunita Verma and myself, we explore how social networks can provide better friend suggestions to users, a challenging practical problem faced by all social network platforms

Friend suggestion – the task of suggesting to a user the contacts she might already know in the network but that she hasn’t added yet – is major driver of user engagement and social connection in all online social networks. Designing a high quality system that can provide relevant and useful friend recommendations is very challenging, and requires state-of-the-art machine learning algorithms based on a multitude of parameters.

An effective family of features for friend suggestion consist of graph features such as the number of common friends between two users. While widely used, the number of common friends has some major drawbacks, including the following which is shown in Figure 1.
Figure 1: Ego-net of Sally.
In this figure we represent the social connections of Sally and her friends – the ego-net of Sally. An ego-net of a node (in this case, Sally) is defined as the graph that contains the node itself, all of the node’s neighbors and the connection among those nodes. Sally has 6 friends in her ego-net: Albert (her husband), Brian (her son), Charlotte (her mother) as well as Uma (her boss), Vincent and Wally (two of her team members). Notice how A, B and C are all connected with each other while they do not know U, V or W. On the other hand U, V and W have all added each other as their friend (except U and W who are good friend but somehow forgot to add each other).

Notice how each of A, B, C have a common friend with each of U, V and W: Sally herself. A friend recommendation system based on common neighbors might suggest to Sally’s son (for instance) to add Sally’s boss as his friend! In reality the situation is even more complicated because users’ online and offline friends span several different social circles or communities (family, work, school, sports, etc).

In our paper we introduce a novel technique for friend suggestions based on independently analyzing the ego-net structure. The main contribution of the paper is to show that it is possible to provide friend suggestions efficiently by constructing all ego-nets of the nodes in the graph and then independently applying community detection algorithms on them in large-scale distributed systems.

Specifically, the algorithm proceeds by constructing the ego-nets of all nodes and applying, independently on each of them, a community detection algorithm. More precisely the algorithm operates on so-called “ego-net-minus-ego” graphs, which is defined as the graph including only the neighbors of a given node, as shown in the figure below.
Figure 2: Clustering of the ego-net of Sally.
Notice how in this example the ego-net-minus-ego of Sally has two very clear communities: her family (A, B, C) and her co-workers (U, V, W) which are easily separated. Intuitively, this is because one might expect that while nodes (e.g. Sally) participate in many communities, there is usually a single (or a limited number of) contexts in which two specific neighbors interact. While Sally is both part of her family and work community, Sally and Uma interact only at work. Through extensive experimental evaluation on large-scale public social networks and formally through a simple mathematical model, our paper confirms this intuition. It seems that while communities are hard to separate in a global graph, they are easier to identify at the local level of ego-nets.

This allows for a novel graph-based method for friend suggestion which intuitively only allows suggestion of pairs of users that are clustered together in the same community from the point of view of their common friends. With this method, U and W will be suggested to add each other (as they are in the same community and they are not yet connected) while B and U will not be suggested as friends as they span two different communities.

From an algorithmic point of view, the paper introduces efficient parallel and distributed techniques for computing and clustering all ego-nets of very large graphs at the same time – a fundamental aspect enabling use of the system on the entire world Google+ graph. We have applied this feature in the “You May Know” system of Google+, resulting in a clear positive impact on the prediction task, improving the acceptance rate by more than 1.5% and decreasing the rejection rate by more than 3.3% (a significative impact at Google scales).

We believe that many future directions of work might stem from our preliminary results. For instance ego-net analysis could be potentially to automatically classify a user contacts in circles and to detect spam. Another interesting direction is the study of ego-network evolution in dynamic graphs.